تعریف توان مختلط

تعریف توان مختلط:
در بسیاری از مراجع، توان AC با کمیت های مختلط بیان می شود؛ زیرا ویژگی های جذابی برای تحلیل دارند (از جبر برداری استفاده می کنند). اما اغلب، «توان مختلط» (Complex Power) به سادگی و بدون استخراج معادلات تعریف می شود. اما اعداد مختلط چگونه کمیت های توان را نشان می دهند؟

در سال 1897، «چارلز پرتیوس استینمتز» (Charles Proteus Steinmetz) در کتابش با نام «نظریه و محاسبه پدیده جریان متناوب»، نمایش شکل موج های AC را با کمیت های مختلط پیشنهاد کرد.

در بخش های قبل، فرم عمومی توان AC را به دست آوردیم (برای ضریب توان پس فاز):

که در آن، V و I مقادیر RMS ولتاژ و جریان هستند.

برای فرکانس زاویه ای ثابتω، این شکل موج را می توان با دو پارامتر مشخص کرد: یکی ضرب ولتاژ مؤثر در جریان مؤثر و دیگری زاویه پس فاز−θ.

با استفاده از این دو پارامتر، می توانیم شکل موج AC توانp(t) را با بردار دو بعدی S بیان کنیم که در مختصات قطبی، با اندازه VI و زاویه قطبی−θ تعریف می شود.

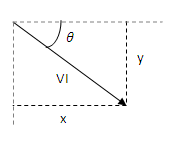
این بردار S را می توان به یک زوج در مختصات دکارتی تبدیل کرد:

با استفاده از مثلثات می توان نشان داد که جمع و تفریق بردارهای توان AC از قواعد کلی حساب برداری تبعیت می کند؛ یعنی مؤلفه های مستطیلی دو یا چند تابع سینوسی را می توان با هم جمع یا از هم کم کرد (اما نمی توان آن ها را در هم ضرب یا بر هم تقسیم کرد).

البته کار با هر مؤلفه مستطیلی به تنهایی می تواند سخت یا غیرممکن باشد. فرض کنید مؤلفه های مستطیلی x و y را با استفاده از عملگر بی معنی j تفکیک کنیم. بنابراین، بردار S به صورت زیر خواهد بود:

توجه کنید که علامت جمع (+) در عبارت بالا یک علامت ساده نیست، زیرا x و y کمیت های متعامدی در فضای دو بعدی هستند. نماد j، یک عملگر بی معنی برای تمایز مؤلفه عمودی y است.

فرض کنید بردار را90∘ می چرخانیم:

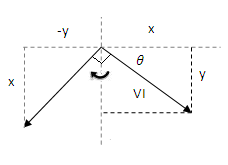
بردار بعد از چرخش به صورت زیر است:

حال عملگر j را برای چرخش 90∘ به گونه ای تعریف می کنیم که ضرب بردار V در j بردار را به اندازه90∘ بچرخاند. بنابراین، داریم:

در نتیجه، با تعریف j به عنوان عملگر چرخش 90 درجه ای، j یک عدد موهومی خواهد بود و بردار S=x+jy یک مقدار مختلط است. بنابراین، بردار S را می توان به صورت زیر نوشت:

عبارت بالا را توان مختلط یا گاهی «توان ظاهری» (Apparent Power) می نامند. توان ظاهری برای ضریب توان پس فاز و پیش فاز به صورت زیر خواهد بود:

برای ضریب توان پس فاز:    
برای ضریب توان پیش فاز:

که در آن،  P=VIcosθ و Q=VIsinθ به ترتیب، مقادیر توان اکتیو (یا حقیقی) و توان راکتیو هستند.