تعریف حالت پلاریزاسیون در مدار:
پلاریزاسیون، به وسیله حالت های مختلف پلاریزاسیون و یک موج همدوس سینوسی در فرکانس نوری قابل درک است.

امواج2

بردار نشان داده شده در شکل زیر، نویان میدان الکتریکی توسط یک لیزر تک مود را نشان می دهد. نوسان های میدان در صفحه xy و انتشار موج در جهت z و عمود بر صفحه میدان است.

شکل زیر، بردار میدان الکتریکی را در یک چرخه کامل برای پلاریزاسیون خطی در دو جهت مختلف نشان می دهد.

هر کدام از این جهت ها، یک حالت پلاریزاسیون مشخص دارند. لازم به ذکر است که پلاریزاسیون خطی در 45 درجه را می توان به صورت جمع یک موج خطی پلاریزه به صورتی افقی و یک موج خطی پلاریزه به صورت عمودی با دامنه و فاز یکسان دید.

حال اگر بین این دو مولفه پلاریزاسیون افقی و عمودی یک جابه جایی فاز داشته باشیم، به «پلاریزاسیون بیضوی» (Elliptical Polarization) می رسیم. هنگامی که جابه جایی فاز دقیقا برابر با±90∘ است، «پلاریزاسیون دایروی» (Circular Polarization) به دست می آید.

بنابراین برای تولید پلاریزاسیون دایروی در عمل، لازم است نور پلاریزه شده به صورت خطی را به یک «صفحه یک چهارم طول موج» (Quarter-Wave Plate) اعمال کنیم. به این ترتیب، جابه جایی فاز±90∘لازم برای ایجاد پلاریزاسیون دایروی ایجاد می شود.

در نتیجه جابه جایی فاز در این دو مولفه، یک بردار میدان الکتریکی چرخان به دست می آید. شکل زیر، این موج را نشان می دهد:

شکل 3

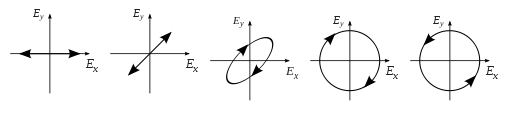
لازم به ذکر است که پلاریزاسیون دایروی یا بیضوی می تواند چرخش میدانی در جهت عقربه های ساعت یا در خلاف جهت عقربه های ساعت داشته باشد. این مسئله به حالت های پلاریزاسیون مشخص منجر می شود.

البته جهت مولفه های x و y استفاده شده در این آموزش، اختیاری است. انتخاب این سیستم مختصاتی و مشاهده بیضی پلاریزاسیون بر حسب مولفه های پلاریزاسیون های x و y، به تعریف بردار جونز بر حسب «پلاریزاسیون های پایه» (Basis Polarization) مربوط است.

برای هر مسئله باید از محورهای عمود بر هم مطابق با آن استفاده کرد. برای مثال، محور x می تواند در صفحه موج برخوردی باشد.

همچنین می توان از جفت توابع پایه متعامد متفاوت برای تعریف حالت های مختلف پلاریزاسیون و نه فقط پلاریزاسیون خطی استفاده کرد.

برای مثال، انتخاب پلاریزاسیون های دایروی چپ و راست به عنوان توابع پایه، حل مسائل مربوط به دو شکستی یا دورنگی دایروی را آسان می کند.