نوسان های اجباری و رزونانس:

اگر مدار رزونانس یا تشدید، شامل یک منبع با emf متغیر متناوب باشد، نوسان های متناوب در سیستم به وجود می آید. اگر نیروی محرکه الکتریکی E منبع متغیر به صورت زیر باشد:

آن گاه معادله دیفرانسیل نوسان های اجباری در مدار RLC سری را می توان به صورت زیر نوشت:

یا

که در آن، q بار خازن است. همچنین تساوی های 2β=RL و ω20=1LC نیز برقرارند.

معادله بالا، متناظر با معادله نوسان اجباری یک جسم متصل به فنر است. جواب این معادله، از مجموع جواب عمومی و جواب خصوصی معادله ناهمگن تشکیل می شود. بخش اول، کاهش گذرا است و بعدی، فقط به نیروی خارجی اعمال شده بر مدار بستگی دارد.

نوسان های اجباری، به صورت زیر خواهند بود:

که در آن، φ با فرمول زیر تعیین می شود:

با دانستن تغییر بارq(t)، به سادگی می توان جریان را نیز محاسبه کرد:

که در آن، زاویه θ جابه جایی فاز نوسان های جریانI(t) را نسبت به نوسانات منبع ولتاژ E(t)=E0cosωt نشان می دهد.

دامنه جریان (I0) و جابه جایی فاز (θ) برابرند با:

کمیت ، امپدانس یا امپدانس مدار نامیده می شود. امپدانس، از مقاومت اهمی R و راکتانس تشکیل می شود. امپدانس مدار رزونانس، به فرم مختلط به صورت زیر نوشته می شود:

با توجه به فرمول های بالا، می توان دریافت که دامنه نوسان حالت ماندگار، وقتی ماکزیمم است که داشته باشیم:

در این شرایط، رزونانس در مدار رخ می دهد. فرکانس رزونانس ω 0 برابر با فرکانس نوسان های آزاد در مدار است و به مقاومت R بستگی دارد.

می توانیم فرمول دامنه نوسان های اجباری را برای به دست آوردن یک وابستگی صریح به نسبت فرکانس تبدیل کنیم که در آن، ω0 فرکانس رزونانس است. در نتیجه، داریم:

وابستگی دامنه جریان به نسبت فرکانس برای مقادیر مختلفrوc در شکل های 4 و 5 نشان داده شده است. این منحنی ها برای پارامترهایE=100V، L=1mH، C=10μF (شکل 4) وR=10ohms (شکل 5)، رسم شده اند.

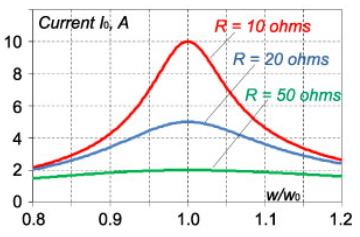
شکل 4

شکل 5

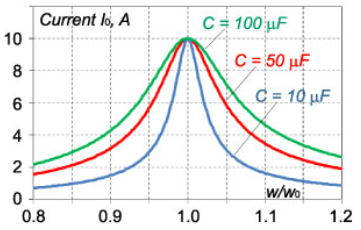
شکل 5
ویژگی های رزونانسی یک مدار، با ضریب کیفیتQ مشخص می شوند که مقدار عددی آن برابر با نسبت فرکانس رزونانسω0 به پهنای Δω مربوط به منحنی رزونانس در حداکثر مقدار است (شکل 6).

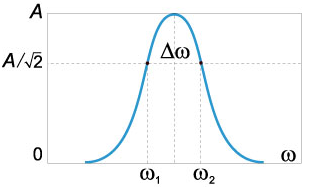
شکل 6