نوسان های میرا در مدار RLC سری:
معادله دیفرانسیل مرتبه دومی که نوسان های میرا را در مدار RLC سری توصیف می کند، به صورت زیر است:
معادله مشخصه متناظر به فرم زیر است:
ریشه های معادله بالا نیز برابرند با:
که در آن، 
ضریب میرایی و ω 0 فرکانس رزونانس مدار است.
بسته به مقادیر R، L و C سه حالت مختلف داریم.
در این حالت، هر دو ریشه معادله مشخصه λ1 و λ2 حقیقی، مجزا و منفی هستند. پاسخ عمومی معادله دیفرانسیل به صورت زیر است
در این مورد، جریان به صورت یکنوا به صفر میل می کند (شکل 3)
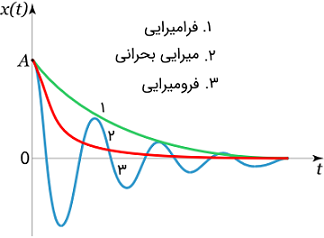
شکل 3
این حالت، مرزی یا بحرانی نامیده می شود. در این جا، ریشه های معادله مشخصه، برابر، حقیقی و منفی هستند. جواب عمومی این حالت، به صورت زیر است:
در ابتدا، جریان ممکن است حتی افزایش نیز پیدا کند، اما به سرعت به صورت نمایی کاهش پیدا می کند.
در این حالت، ریشه های معادله مشخصه مزدوج مختلط هستند و منجر به نوسان های میرا در مدار می شوند. جریان به صورت زیر به دست می آید:
که در آن، 
ضریب میرایی، و 
فرکانس نوسان، و A و B ثابت های انتگرال گیری هستند و به شرایط اولیه بستگی دارد. توجه کنید که فرکانس ω کمتر از فرکانسω 0 رزونانس مدار است. شکل عمومی منحنی I(t) در این حالت، در شکل 3 نشان داده شده است.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
