معادلات دیفرانسیل مدارهای RLC:
در مدارهایی شامل مقاومت (R)، سلف (L) و خازن (C) می توان نوسان های الکتریکی را مشاهده کرد.
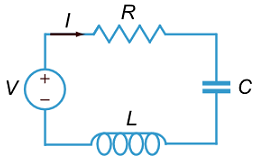
دو مداری که در این رابطه مورد توجه قرار می گیرند، مدارهای RLC سری (شکل 1) و RLC موازی (شکل 2) هستند.
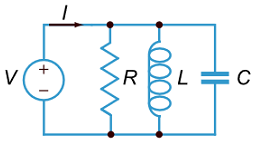
شکل 2
معادلات دیفرانسیل مدار RLC سری:
ابتدا، معادلات مدار RLC سری را با توصیف تغییرات جریان در مدار RLC سری می نویسیم.
ولتاژهای VR، VC و VL به ترتیب، اختلاف پتانسیل دو سر مقاومتR، خازن C و سلف L را نشان می دهند. روابط این متغیرها به صورت زیر است:
طبق قانون ولتاژ کیرشهف (KVL)، داریم:
که در آن، E(t) نیروی محرکه الکتریکی (emf) منبع توان است.
وقتی مقدار emf ثابت باشد (E)، بعد از جایگذاری عبارت های VR، VC و VL در معادله دیفرانسیل و مشتق گیری از این معادله، داریم:
با تعریف 
، معادله را می توان به صورت زیر بازنویسی کرد:
معادله دیفرانسیل بالا، مشابه معادله نوسان های میرای جرم متصل به فنر است. بنابراین، نوسان میرا در مدارهای RLC با مقادیر خاصی برای پارامترها رخ می دهد.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
