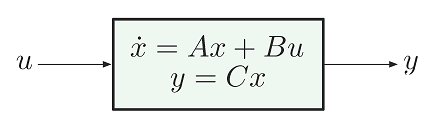جایابی قطب در سیستم

جایابی قطب:

سیستم فضای حالت زیر را در نظر بگیرید:

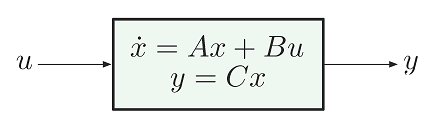
مدل فضای حالت یک سیستم با ورودی $$u$$ و خروجی $$y$$

شکل 1: مدل فضای حالت یک سیستم با ورودیu و خروجy

که در آن، ماتریس D را برابر با صفر در نظر گرفته ایم. فرض می کنیم سیستم مورد نظر کاملاً کنترل پذیر است.

سیستم را کنترل پذیر (Controllable) می گوییم اگر همیشه یک ورودی کنترل u وجود داشته باشد که با آن بتوان حالت های سیستم را در زمان محدود به وضعیت جدید دیگری انتقال داد.

به طور خاص، یک سیستم LTI کنترل پذیر است اگر و فقط اگر رتبه (Rank) ماتریس کنترل پذیریC کامل باشد (یعنی اگر تعداد حالت های سیستم را n فرض کنیم، رتبه ماتریس Cباید برابر باnباشد).

ماتریس کنترل پذیری (Controllability Matrix) برای سیستمی با ماتریس حالتAو ماتریس ورودیB به صورت زیر تعریف می شود:

رتبه یک ماتریس با تعداد سطرها یا ستون هایی از ماتریس که از یکدیگر استقلال خطی دارند متناظر است.

به بحث جایابی قطب بر می گردیم. تابع تبدیلG(s)متناظر با شکل 1 به صورت زیر است:

قطب های حلقه باز سیستم، مقادیر ویژه ماتریسA هستند:

در حالت کلی، برای جایابی قطب های سیستم، یک کنترل کننده به آن اضافه می کنیم و می توانیم آن را به صورت های مختلف نشان دهیم.

برای مثال، در فضای تابع تبدیل، نمایش بلوکی سیستم کنترل فیدبک واحد منفی با سیستم تحت کنترلG(s) و کنترل کنندهKD(s) مطابق شکل زیر است.

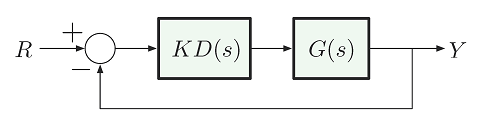
جایابی قطب با کنترل‌کننده $$ K D ( s) $$