محاسبات مربوط به عملکرد موتور

محاسبات مربوط به عملکرد موتور:
با داشتن مدار معادل ساده شده می توانیم محاسبات مربوط به عملکرد یک موتور القایی را انجام دهیم.

توجه کنید که محاسبات پارامترها به صورت برداری است و برای آنکه جابه جایی فاز، ضریب توان و… از محاسبات حذف شود، باید از نمایش مختلط یا فازوری استفاده کنیم.

جریان موتور:
وقتی پارامترهای مدار معادل موتور را به دست آوردیم، می توانیم با ساده کردن مدار معادل به امپدانس Zeq(یا استفاده از امپدانس تونن معادل) به سادگی جریان موتور را به دست آوریم:

با توجه به مدار معادل، Zeq برابر است با:

از این معادله می توان دریافت که با افزایش سرعت روتور (کاهش لغزش)، امپدانس مدار افزایش و جریان استاتور کاهش پیدا می کند.

توان موتور:
اگر، برای ساده سازی، از تلفات هسته (Rc) چشم پوشی کنیم، خواهیم داشت:Is=I′2. در این حالت، توانی که به موتور تحویل داده می شود (Pin)، در هر فاز برابر است با:

توان تلف شده در سیم پیچ ها نیز به صورت زیر به دست می آید:

اختلاف بین توانی که موتور را تغذیه می کند و توان تلف شده در سیم پیچ ها، برابر با توانی است که به بار منتقل می گردد (Pm). این توان در هر فاز برابر است با:

و برای هر سه فاز داریم:

گشتاور موتور:
با دانستن این نکته که توان موتور برابر با ضرب گشتاور موتور (M) در سرعت زاویه ای (ω) است، می توانیم گشتاور (T) را به صورت زیر فرمول بندی کنیم:

و

با ترکیب فرمول توان موتور در معادله گشتاور، داریم:

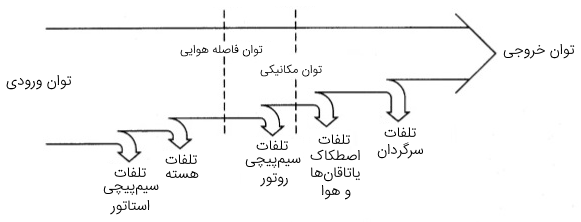
نمودار پخش توان:
در بخش های قبلی درباره نحوه محاسبه پارامترهای مختلف موتور با استفاده از مدار معادل ساده شده و نیز چشم پوشی از تلفات آهن هسته بحث کردیم. برای دقت بیشتر در محاسبات، می توانیم تلفات آهن هسته را نیز در نظر بگیریم.

با توجه به مواردی که گفته شد، نمودار پخش توان موتور القایی مطابق شکل 4 است.