قضیه میلمن

قضیه میلمن:
قضیه میلمن برای ساده کردن مدارهایی مشابه شکل 1 به کار می رود که منبع ولتاژ دارند. هرچند از سایر قضایایی که در مدار وجود دارد می توان برای ساده سازی چنین مداری استفاده کرد، اما قضیه میلمن بسیار ساده تر بوده و مدار معادل را مستقیماً نتیجه می دهد.

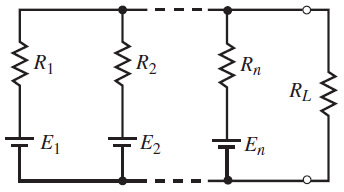
در مدارهایی مانند مدار شکل 1، منابع ولتاژ را می توان با یک منبع معادل، مطابق شکل 2 جایگزین کرد.

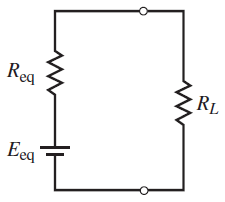
برای پیدا کردن اندازه منبع ولتاژ معادل Eeq و مقاومت سری Req، باید هر یک از منابع ولتاژ شکل 1 را با استفاده از قضیه تبدیل منابع به منبع جریان معادلش تبدیل کرد.

مقدار هر منبع جریان را می توان با استفاده از قانون اهم تعیین کرد (یعنیI1=E1/R1، I2=E2/R2و…). پس از آنکه تبدیل منابع به پایان رسید، مدار به صورت شکل 3 در خواهد آمد.

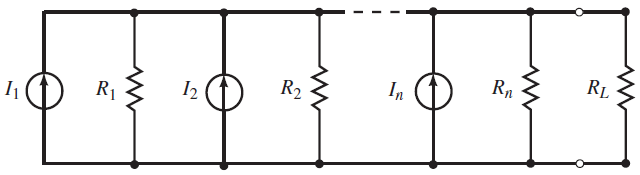
در مدار شکل 3 می بینیم که همه منابع جریان جهت یکسانی دارند. واضح است که همیشه جهت منابع جریان با یکدیگر برابر نیست و جهت آن ها با توجه به پلاریته منبع ولتاژ متناظر تعیین می شود.

اکنون می توانیم n منبع جریان را با یک منبع جریان جایگزین کنیم که مقدار آن برابر است با:

و می توان آن را به صورت زیر نوشت:

اگر جهت هر منبع جریان مخالف جهت نشان داده شده باشد، اندازه آن منبع در فرمول های بالا به جای به علاوه، علامت منها خواهد داشت. از شکل 3 می توان مشاهده کرد که حذف منابع جریان منجر به مقاومت معادل زیر خواهد شد:

که به صورت زیر تعیین می شود:

فرمول کلی ولتاژ معادل، برابر است با:

مثال:
از قضیه میلمن برای ساده کردن مدار شکل 4 به گونه ای استفاده می کنیم که فقط یک منبع داشته باشیم. از مدار ساده شده برای تعیین جریان مقاومت بار RL کمک می گیریم.

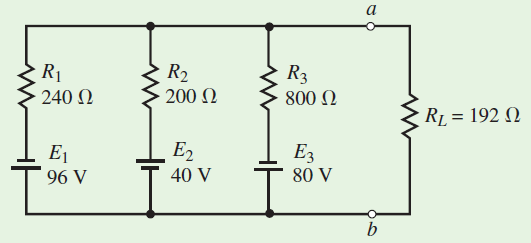
حل: با استفاده از معادله (5) اندازه منبع ولتاژ را به صورت زیر محاسبه می کنیم:

مقاومت معادل برابر است با:

مدار معادل با استفاده از قضیه میلمن در شکل 5 نشان داده شده است. لازم به ذکر است که پلاریته منبع ولتاژ معادل، مخالف پلاریته مفروض اولیه است. این به آن دلیل است که اندازه منابع ولتاژ E1 و E3 به گونه ای است که بر پلاریته و اندازه منبع E2 غلبه می کنند.

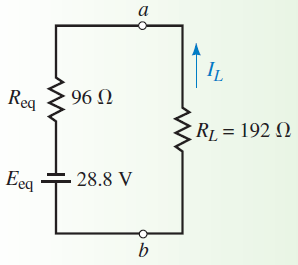
با توجه به مدار شکل 5، به سادگی می توان جریان گذرنده از مقاومت بار را محاسبه کرد:

جهت این جریان به سمت بالا است.