قضیه هم پاسخی برای منابع ولتاژ مستقل

قضیه هم پاسخی برای منابع ولتاژ مستقل:
قضیه هم پاسخی (Reciprocity Theorem) در مدارهای الکتریکی با تنها یک منبع ولتاژ یا جریان مستقل مطرح می شود. این قضیه برای منابع وابسته ولتاژ و جریان قابل استفاده نیست، اما هم به منابع ولتاژ مستقل و هم به منابع جریان مستقل قابل اعمال است.

فرض کنید منبع ولتاژ مستقل یک مدار الکتریکی در شاخه nام آن جریان الکتریکیI را تولید کند (منظور از شاخه یک مسیر برای عبور جریان الکتریکی است).

حال اگر محل منبع ولتاژ مستقل را تغییر دهیم به صورتی که از محل اولیه برداشته شده و به شاخه nام منتقل شود، آنگاه منبع ولتاژ مستقل (در محل جدید) در محل قبلی خود جریانی تولید می کند. این جریان برابر با جریان شاخه nام ناشی از منبع ولتاژ مستقل در محل قبلی است.

هنگام استفاده از قضیه هم پاسخی برای منبع ولتاژ مستقل گام های زیر طی می شود:

• منبع ولتاژ مستقل در محل قبلی اتصال کوتاه می شود. به عبارت دیگر، آن را از مدار بر می داریم و دو سر آن را با یک سیم اتصال کوتاه می کنیم.
• پلاریته منبع ولتاژ مستقل در محل جدید مطابق با پلاریته جریان شاخه است. پلاریته طوری درنظر گرفته می شود که جریان از قطب منفی منبع ولتاژ وارد و از قطب مثبت خارج شود.

مثالی از قضیه هم پاسخی برای منبع ولتاژ مستقل:
حال با یک مثال قضیه را بیشتر توضیح می دهیم. مدار الکتریکی زیر را در نظر بگیرید. این مدار شامل یک منبع ولتاژ مستقل 22 ولتی و سه مقاومت 4، 8 و 12 اهمی است که در اینجا منظور از شاخه nام، مقاومت 12 اهم است که جریان آن را با I و جریان منبع مستقل را با Iin نشان می دهیم.

در قدم اول این جریان را محاسبه می‏ کنیم.

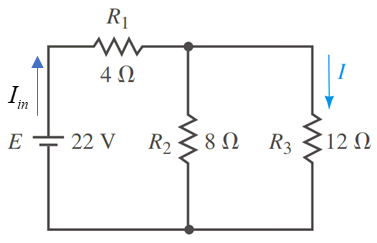
مدار الکتریکی

ابتدا مقاومت دو سر منبع ولتاژ را به دست می آوریم:

سپس جریان عبوری از منبع ولتاژ مستقل را محاسبه می کنیم:

دقت کنید که مقاومت های 12 و 8 اهم یک مدار مقسم جریان را تشکیل می دهند. جریان مقاومت 12 اهم از رابطه زیر به دست می آید:

حال قضیه هم پاسخی را به مدار اعمال می کنیم. منبع ولتاژ مستقل اتصال کوتاه و به صورت سری با مقاومت 12 اهم (همان محل جریان I در مدار قبلی) قرار داده می شود. مدار جدید در شکل زیر نمایش داده شده است.

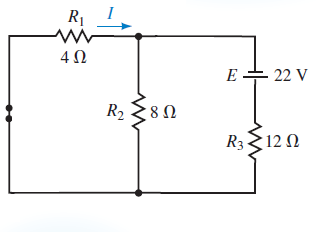
برای محاسبه جریان I در مدار جدید، باز هم ابتدا مقاومت دو سر منبع ولتاژ مستقل را محاسبه می کنیم:

سپس جریان منبع مستقل به صورت زیر محاسبه می شود:

برای محاسبه جریانI، دقت کنید که این بار مقاومت های 4 و 8 اهم مقسم جریان تشکیل می دهند. جریان مقاومت 4 اهم (محل منبع ولتاژ مستقل در مدار قبلی) به صورت زیر تعیین می شود:

کاملا واضح است که این جریان برابر جریان مقاومت 12 اهم در مدار اولی است. بنابراین با این مثال، قضیه هم پاسخی برای منابع ولتاژ مستقل اثبات می شود.