مدل های سیگنال بزرگ و سیگنال کوچک در مبدل

مدل های سیگنال بزرگ و سیگنال کوچک در مبدل:
رفتار دینامیکی مبدل، جز در موارد نادر، غیرخطی است. گاهی اوقات برای تحلیل مُدال (Modal Analysis) یا طراحی قوانین کنترل خطی، باید مدل را حول یک نقطه کار معین خطی کرد.

بدین منظور، از بسط سری تیلور مرتبه اول استفاده می شود. مدل های خطی شده فقط برای تغییرات اندک حول نقطه کار مورد نظر معتبر هستند.

به همین دلیل، این مدل ها را مدل سیگنال کوچک یا مدل مماسی خطی (Tangent Linear Model) می نامند.

برخلاف مدل های خطی، مدل های اولیه که آن ها را مدل های سیگنال بزرگ می نامند، در کل محدوده تعریف معتبر هستند.

شکل 8 ارتباط بین مدل سیگنال بزرگ و مدل سیگنال کوچک را برای مسیر حالت یک سیستم مرتبه دوم نشان می دهد.

اگر مدل سیگنال بزرگ خطی باشد، آنگاه با مدل سیگنال کوچک یکسان خواهد بود. این وضعیت به ندرت رخ می دهد. مبدل کاهنده ایده آل با بار ثابت از این موارد است. این رویکرد، مشابه مدل سازی میانگین و نمونه برداری است.

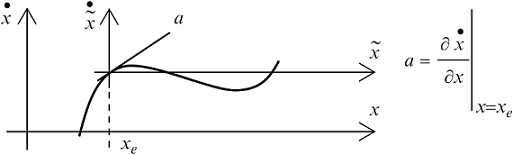
شکل 8: ارتباط بین مدل سیگنال بزرگ و مدل سیگنال کوچک یک سیستم مرتبه دوم در فضای حالت
فرم کلی سیستم غیرخطی پیوسته زیر را درنظر بگیرید:

که در آن، x، uوy به ترتیب بردارهای حالت، ورودی و خروجی هستند.

محاسبه مدل حالت ماندگار:
با صفر قرار دادن مشتقات می توان مشخصه ورودی-خروجی، یعنی مکان هندسی نقاط تعادل را در حالت ماندگار به دست آورد. این نقاط با زیرنویسe نوشته شده و با یک منحنی غیرخطی عمومی در صفحه ورودی-خروجی نمایش داده می شوند:

تشکیل مدل سیگنال کوچک:
اکنون تغییرات کوچک ~x=x−xe، ~u=u−ue و ~y=y−ye را حول نقطه تعادل y e درنظر بگیرید که پاسخ ورودی ue است. سیستم خطی شده حول این نقطه تعادل را می توان به شکل زیر نوشت:

که

برای سیستم های دو خطی، یعنی سیستم هایی که غیرخطی بودن آن ها ضرب بین دو متغیر حالت یا بین متغیر حالت و متغیر ورودی است، یک روش دیگر استفاده می شود که در ادامه می آید.

تغییرات کوچک فوق را می توان در مدل رابطه (8) وارد کرده و ساده سازی های زیر را انجام داد:

• چشم پوشی از ضرب تغییرات متناظر با جملات مرتبه بالاتر از 2 در بسط سری های تیلور.
• ساده سازی جملات متناظر باx=0.

مدل حاصل، مشابه مدل خطی شده (9) با ماتریس های (10) است.

در اینجا یک مثال ساده را بررسی می کنیم. معادله (11) یک سیستم دو خطی را نشان می دهد. از دو روش بالا برای به دست آوردن مدل سیگنال کوچک استفاده می کنیم.

ابتدا نقطه تعادل سیستم را برای ورودی u=ue به دست می آوریم. این کار با صفر قرار دادن مشتق متغیرهایx1 و x2 انجام می شود.

با حل سیستم جبری، دو جواب به دست می آید. برای جواب اول، واضح است کهx1e=x2e=0 و نتیجه می دهدye=ue. نقطه دیگرx1e=ue/2 و x2e=−ue/2است که درنتیجهye=3ue/4.

در گام دوم باید ماتریس های مدل خطی شده سیستم را محاسبه کنیم. برای این کار، می توان از دو روش استفاده کرد:

روش اول: استفاده از روابط (10) برای محاسبه ماتریس های C، B، A و D:

روش دوم: با جایگذاری تغییرات سیگنال کوچک~x=x−xeکه در آن،    در مجموعه روابط (11)، داریم:

در حالت ماندگار، سیستم با روابط (13) توصیف می شود:

با انجام ضرب ها و چشم پوشی از ضرب تغییرات~x1⋅~x2، ~x21و~x2⋅~uو دانستن˙x1e=˙x2e=0 و نیز با توجه به رابطه (13) می توان نوشت:

با استفاده از معادله (13) می توان مقادیر حالت ماندگار متغیرهای حالت را به عنوان توابعی ازueو به صورت x1e=ue/2وx2e=−ue/2 محاسبه کرد. با جایگذاری این مقادیر، رابطه (14) به شکل زیر در می آید:

که ماتریس های C، B، A و D همان هایی هستند که از روش اول به دست آمده اند.

مدل سیگنال کوچک را می توان در حوزه فرکانس یعنی به صورت تابع تبدیل نیز نمایش داد که با استفاده از ماتریس های استخراج شده بالا، به شکل زیر محاسبه می شود:

که در آن~U(s)و~Y(s) به ترتیب تبدیلات لاپلاس سیگنال های زمانی اسکالر~uو~y هستند. با اعمال تبدیل لاپلاس به معادله (15) می توان به توصیف مشابهH(s)دست یافت. با معرفی~X1(s)و~X2(s) به عنوان تبدیل لاپلاس متغیرهای حالت مدل سیگنال کوچک، داریم:

توجه کنید که ~x2 یک حالت مشاهده ناپذیر است، زیرا در خروجی ظاهر نشده و ناپایدار نیز هست.