اصول کنترل پیش بین مدل (MPC):
کنترل پیش بین مدل بر اساس بهینه سازی تکراری (آنلاین) یک تابع هزینه با افق محدود از عملکرد پلانت کار می کند.
شکل زیر اصول کار این کنترل کننده محبوب را نشان می دهد. فرض کنید که وضعیت تمام سیگنال های موجود در سیستم تا نمونه kام در دسترس باشد، یعنی حالت ها و خروجی های سیستم از نمونه 0 تا نمونه kام و همچنین سیگنال کنترلی نیز از نمونه 0 تا k−1 ام در دسترس باشند.
دقت کنید که اگر زمان نمونه بردای مشخص باشد، شماره نمونه به راحتی تبدیل به زمان واقعی خواهد شد (t=kTs). به همین دلیل از این به بعد به جای نمونه از زمان استفاده می کنیم تا درک مطلب واضح تر شود.
حال هدف این است که سیگنال های کنترلی از زمان k تا زمانk+p را طوری تعیین کنیم، که خروجی سیستم از زمان k تا زمان k+p تا حد ممکن به خروجی مرجع نزدیک باشد.
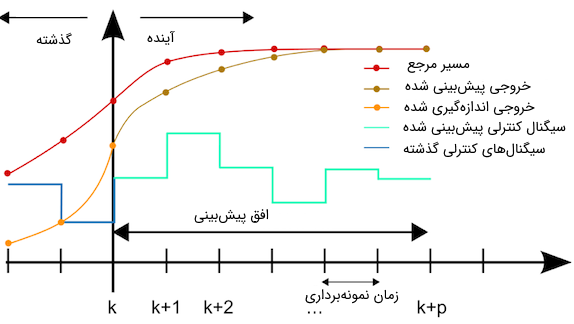
برای این کار باید خروجی سیستم از زمانkتا زمانk+p پیش بینی شود، که با توجه به مشخص بودن مدل دینامیکی سیستم، به راحتی می توان پیش بینی را انجام داد.
به پارامترp افق پیش بینی گفته می شود و در واقع طول بازه پیش بینی را نشان می دهد. اگر فرض کنیم که مدل دینامیکی گسسته سیستم به صورت زیر باشد:
آنگاه با توجه به اینکه اطلاعات خروجی سیستم تا زمانkو اطلاعات سیگنال کنترلی تا زمانk−1 مشخص است، پس خروجی یک نمونه به جلو یا یک گام به جلو به صورت زیر خواهد بود:
از علامتˆyبرای نشان دادن مقادیر پیش بینی استفاده می شود وˆy(k+1∣k) به معنی پیش بینی یک گام به جلو با داشتن اطلاعات تا زمان k است. حال با جایگذاریk+1به جایk در رابطه بالا پیش بینی دو گام به جلو به دست می آید:
به همین ترتیب، با جایگذاری های متوالی، پیش بینی تاp گام به جلو انجام می شود.
واضح است که تمام پیش بینی ها، وابسته به سیگنال کنترلی در طول افق پیش بین (یعنیu(k) تا u(k+p−1)) هستند. حال برای اینکه پیش بینی ها تا حد امکان به خروجی های مرجع نزدیک باشند، اغلب از تابع هزینه مجموع مربعات خطای ردیابی استفاده می شود. خطای ردیابیn گام به جلو به صورت زیر تعریف می شود:
که در آن n می توان از یک تاpتغییر کند و yref(k+n) مقدار سیگنال مرجع می باشد. حال مجموع مربعات خطا به صورت زیر تعریف می شود:
با بهینه سازی تابع هزینه بالا، سیگنال کنترلی در طول افق پیش بین به دست می آید. اما همان طور که قبلا اشاره شد، علاوه بر حداقل سازی تابع هزینه باید قیدهای فیزیکی نیز برآورده شوند. بهینه سازی تابع هزینه بالا ممکن است منجر به سیگنال کنترلی با دامنه بالا شود.
برای رفع این مشکل، انرژی سیگنال کنترلی در طول افق پیش بین نیز به تابع هزینه اضافه می شود:
جمله دوم در تابع هزینه، باعث می شود که مصالحه ای بین دامنه سیگنال کنترلی و خطای ردیابی برقرار شود.
پارامترρ به منظور تنظیم اهمیت نسبی خطای ردیابی نسبت به دامنه سیگنال کنترلی استفاده می شود. هرچه خطای ردیابی نسبت به دامنه سیگنال کنترلی اهمیت بیشتری داشته باشد، اندازهρ کوچک تر انتخاب می شود.
مسئله بهینه سازی بالا نامقید است و اگر بخواهیم قید سیگنال کنترلی صد در صد رعایت شود، باید مسئله بهینه سازی مقید زیر را محاسبه کنیم:
حال اگر خروجی های پیش بینی شده نیز مقید باشند (مثلا سرعت موتور هیچ وقت بزرگ تر از 1000 دور بر دقیقه نشود)، مسئله بهینه سازی به صورت زیر تغییر پیدا می کند:
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
