مسئله از دیدگاه فیلتر کالمن

مسئله از دیدگاه فیلتر کالمن چگونه است؟

حالت ساده ای را در نظر بگیرید که فقط از موقعیت و سرعت تشکیل شده است:

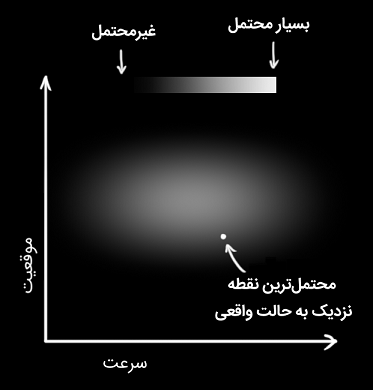
موقعیت و سرعت واقعی را نمی دانیم و طیف وسیعی از ترکیب های موقعیت و سرعت وجود دارند که می توانند درست باشند، اما تعدادی از آن ها نسبت به سایرین به واقعیت نزدیک ترند.

در فیلتر کالمن، فرض می شود که دو متغیر (در مثال ما، موقعیت و سرعت) تصادفی هستند و به صورت گوسی توزیع شده اند. هر متغیر یک مقدار میانگین (Mean) با نمادμ دارد که مرکز توزیع تصادفی (محتمل ترین حالت) است.

متغیرها یک مقدار واریانس (Variance) با نماد σ2 نیز دارند که معرف نامعینی است. شکل زیر، این موضوع را به خوبی نشان می دهد.

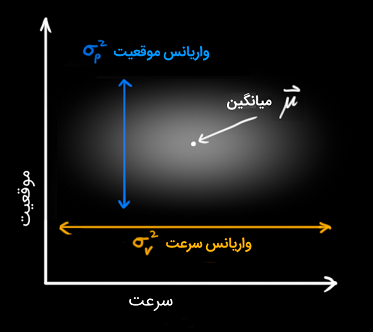
در شکل بالا، موقعیت و سرعت ناهمبسته (Uncorrelated) هستند. این بدین معنی است که وضعیت یک متغیر، اطلاعاتی درباره متغیر دیگر به دست نمی دهد.

شکل زیر، مورد جذاب تری را نشان می دهد که در آن، موقعیت و سرعت همبسته (Correlated) هستند. بنابراین، احتمال مشاهده یک موقعیت خاص به سرعت بستگی خواهد داشت.

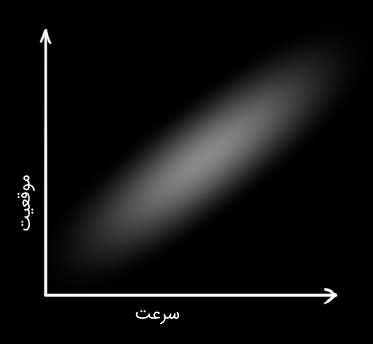
اگر برای مثال بخواهیم موقعیت جدید را بر اساس موقعیت قبلی تخمین بزنیم، این مورد (همبستگی) وجود خواهد داشت. اگر سرعت زیاد باشد، احتمالاً مسافت بیشتری پیموده می شود و در نتیجه، موقعیت دورتر خواهد بود. اگر به آرامی حرکت کنیم، به اندازه کمی دور خواهیم شد.

این رابطه بسیار مهم است، زیرا اطلاعات بیشتری به ما می دهد. به عبارت بهتر، یک اندازه گیری، اطلاعاتی را درباره سایر متغیرها ارائه می کند. هدف فیلتر کالمن نیز همین است که می خواهیم در حد امکان، اندازه گیری های نامعین را به عنوان اطلاعاتِ بیشتر، فشرده کنیم.

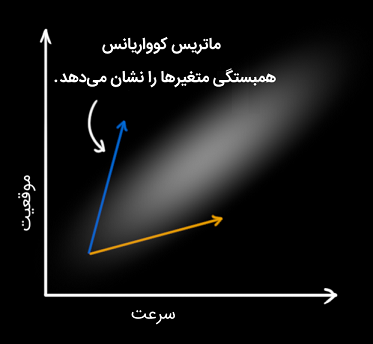
همبستگی را می توان در قالبی به نام ماتریس کوواریانس (Covariance Matrix) نشان داد. به طور خلاصه، هر درایه Σij از ماتریس کوواریانس، درجه همبستگی بین متغیر حالتiاُم و متغیر حالت j اُم را نشان می دهد.

احتمالاً دریافته اید که به دلیل رابطه دوطرفه متغیرهای حالت، ماتریس کوواریانس متقارن (Symmetric) است. ماتریس کوواریانس را معمولاً با Σ و  درایه های آن را با Σij نشان می دهند.