تحلیل حالت دائمی سینوسی در مدارت الکتریکی

تحلیل حالت دائمی سینوسی در مدارت الکتریکی:
تحلیل حالت دائمی سینوسی یکی از روش های بسیار مهم در تجزیه و تحلیل مدارت الکتریکی AC است.می دانیم که قوانین اهم (Ohm) و کیرشهف (Kirchhoff) در مدارات AC نیز قابل اعمال هستند.

روش های تحلیل مش و تحلیل گره نیز در مدارات DC قبلا توضیح داده شده اند. در این مطلب قصد داریم به بررسی تحلیل حالت دائمی سینوسی و نحوه اعمال روش های تحلیل مش و تحلیل گره در مدارات AC بپردازیم.

تحلیل مدارات AC همیشه در سه گام اساسی انجام می گیرد:

• ابتدا باید مدار به حوزه فرکانسی یا فازوری انتقال داده شود.
• مسئله با استفاده از تکنیک های مداری مانند تحلیل مش و تحلیل گره و یا جمع آثار حل شود.
• جواب های به دست آمده در حوزه فرکانسی به حوزه زمان منتقل شوند.

توجه کنید که اگر مسئله خود در حوزه زمان مطرح شده باشد، از گام اول صرف نظر می شود.

در گام دوم تحلیل مدار دقیقا مانند آن چه در مدارات DC انجام می گرفت، تکرار می شود و تنها تفاوت در وجود اعداد مختلط در محاسبات حوزه فرکانس است. حال به بررسی روش تحلیل گره در تحلیل حالت دائمی سینوسی می پردازیم.

آنالیز گره در تحلیل حالت دائمی سینوسی:
اساس روش آنالیز گره بر قانون جریان کیرشهف استوار است. از آن جا که قانون KCL در مورد فازورها هم قابل اعمال است، در نتیجه می توان برای تحلیل مدارات AC از روش تحلیل گره استفاده کرد. در مثال زیر به بررسی نحوه اعمال این روش می پردازیم.

مثال 1:
در مدار زیرixرا با استفاده از روش تحلیل گره بیابید.

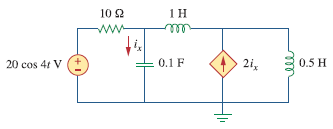
حل: ابتدا مدار را به حوزه فرکانس منتقل می کنیم.

بنابراین مدار معادل فرکانسی به صورت زیر خواهد بود.

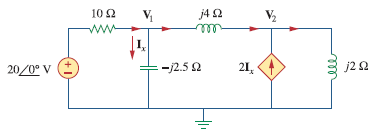
حال در گره 1 KCL اعمال می کنیم.

معادله بالا را بازنویسی می کنیم.

با اعمال KCL در گره شماره 2 داریم:

از طریق جایگذاری در معادله بالا داریم:

پس از ساده کردن معادله بالا داریم:

معادلات بالا را می توان به فرم ماتریسی نیز نوشت.

حال باید دترمینان ماتریس را به دست بیاوریم.

دستگاه معادلات بالا را می توان به روش کرامر حل کرد.

در نتیجه جریان Ix را می توان به صورت زیر به دست آورد:

در نهایت باید جواب به دست آمده را به حوزه زمان منتقل کنیم.

آنالیز مش در تحلیل حالت دائمی سینوسی:
قانون ولتاژ کیرشهوف پایه و اساس روش تحلیل مش را شکل می دهد. این روش را می توان در مدارات AC نیز به کار برد. توجه کنید که روش تحلیل مش را باید در مدارات مسطح دو وجهی (Planar) به کار برد. حال نحوه اعمال این روش را در مثال زیر بررسی می کنیم.

مثال 2:
جریانIoرا در مدار شکل زیر از طریق روش تحلیل مش به دست آورید.

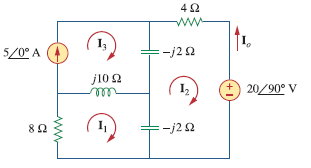
مدار مثال
حل: قانون KVL را در مش 1 اعمال می کنیم.

در مش شمار 2 نیز قانون KVL را اعمال می کنیم.

جریان I3 در مش شماره 3 برابر با 5 آمپر است. این مقدار را در معادلات بالا جایگذاری می کنیم.

این معادلات را می توانیم به فرم ماتریسی بازنویسی کنیم.

حال مانند مثال قبل دترمینان ماتریس را به دست می آوریم.

دستگاه معادلات را به روش کرامر حل می کنیم.

حال جریان Io را می توان به صورت زیر به دست آورد.