کاربردهای کو انرژی (سیستم دوار با تحریک تکی)

کاربردهای کو انرژی (سیستم دوار با تحریک تکی):
یک سیستم دوار با تحریک تکی را در نظر بگیرید که در شکل 8 نشان داده شده است. یک جریان سینوسی به سیم پیچی استاتور اعمال شده و روتور آزادانه روی شفت می چرخد.

گشتاور گشترش یافتهTرا می توان از متغیرهایiوθ و با معادله زیر محاسبه کرد:

لازم به ذکر است که فرکانس جریان استاتور (ω) با فرکانس چرخش مکانیکی (ωm) متفاوت است.

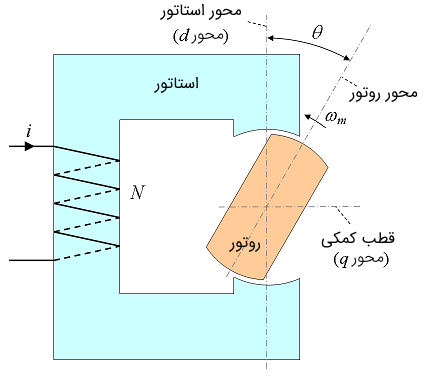
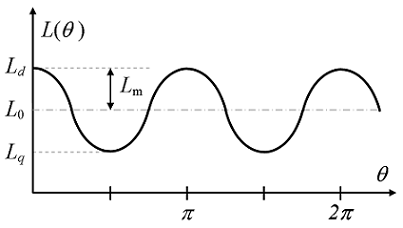
رلوکتانس تابعی از موقعیت روتور است و به دلیل تقارن، دو چرخه رلوکتانس در یک چرخش کامل روتور وجود دارد. در این حالت خاص، رلوکتانس و در نتیجه تغییرات اندوکتانس را می توان با تابع ساده زیر توصیف کرد (شکل 9):

به دلیل وجود یک فاصله هوایی نسبتاً قابل توجه، سیستم خطی بوده و کو انرژی (که در این حالت برابر با انرژی است) از معادله زیر محاسبه می شود:

سپس گشتاورTd(برای محورd در شکل 8) را می توان محاسبه کرد:

و با استفاده از تابع معلوم اندوکتانس (معادله (20) و معادله جریان (19))، داریم:

فرض بر این است که روتور در سرعت زاویه ای ωm می چرخد (شکل 8). بنابراین، داریم:

در لحظهt=0، با تعریف معادله (19)، رابطهi=0 را داریم. در نتیجه، موقعیت روتور برابر است با:

بنابراین، معادله (23) را می توان با اتحادهای مثلثاتی برای sin2(x)وsin(y)⋅sin(z) بازنویسی کرد:

مقدار میانگین یک تابع سینوسی برابر با صفر است. تنها حالتی کهTd,avg صفر نیست، برابری دو فرکانس (ωm=ω) است:

از شکل 9 مشخص استLm دامنه تغییرات اندوکتانس است که در این حالت، به صورت زیر محاسبه می شود:

بنابراین، گشتاور گسترش یافته میانگین برای این حالت خاص به صورت زیر خواهد بود:

محاسبات مشابهی را می توان برای یک سیستم دوار با تحریک چندگانه نیز انجام داد، اما همه جریان ها و اندوکتانس ها (همچنین اندوکتانس های متقابل) را باید در محاسبات در نظر گرفت.