ریاضیات مدولاسیون فرکانس

ریاضیات مدولاسیون فرکانس:

سیگنال پیامی که قرار است منتقل شوند راx(m(t) فرض کرده و سیگنال حامل سینوسی را با معادله زیر نشان می دهیم:

در فرمول بالا، fc فرکانس پایه سیگنال حامل وA c دامنه سیگنال حامل است. مدولاسیون فرکانس، سیگنال حامل را با سیگنال پیام باند پایه (Baseband Data Signal) ترکیب می کند و در نهایت سیگنال مدولاسیون به صورت زیر به دست می آید که قابل انتقال تا مسافت های طولانی است.

در فرمول بالا، f△=kfAm است که در آنkf حساسیت مدولاتور فرکانس وAm دامنه سیگنال پیام یا سیگنال باند پایه را نشان می دهد.

در این معادلهfτ، فرکانس لحظه ای اسیلاتور وf△ انحراف فرکانسی است. انحراف فرکانسی نشان دهنده بیشینه انتقال نسبت بهfc در یک جهت است، با این فرض کهxm(t)در بازه±1 محدود باشد.

نمایی از سیگنال پیام، سیگنال حامل و سیگنال مدوله شده توسط مدولاسیون فرکانس در تصویر زیر نشان داده شده اند.

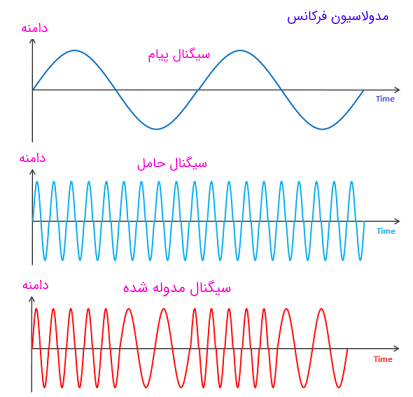
به دلیل این که قسمت عمده انرژی سیگنال درfc±f△ است، از طریق آنالیز فوریه می توان نشان داد که گستره وسیعی از فرکانس ها مورد نیاز است تا بتوان یک سیگنال FM را با دقت بالا نمایش داد.

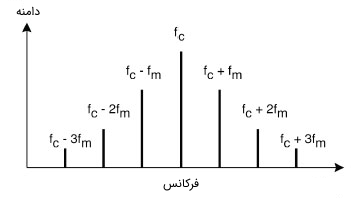
طیف فرکانسی متعلق به یک سیگنال FM واقعی، دارای المان هایی است که تا بی نهایت بسط داده شده اند، البته دامنه این المان ها به تدریج کاهش می یابند و از المان های مراتب بالا معمولا در مسائل طراحی عملی صرف نظر می شود.

در تصویر زیر نمایی از طیف فرکانسی متعلق به یک سیگنال FM نشان داده شده است.

سیگنال باند پایه سینوسی:
از لحاظ ریاضی، سیگنال پیام باند پایه را می توان با موج پیوسته سینوسی تقریب زد که دارای فرکانسfm باشد. این روش، مدولاسیون تک تن (Single-Tone Modulation) نیز نامیده می شود. انتگرال چنین سیستمی برابر است با:

در این حالت، می توان معادلهy(t) به دست آمده در قسمت قبل را به صورت زیر بازنویسی کرد:

در این فرمول، دامنه Am سیگنال سینوسی باند پایه، توسط انحرافf△ نمایش داده می شود. توزیع هارمونیک سیگنال حامل سینوسی که توسط چنین سیگنال باند پایه سینوسی مدوله شده باشد را می توان با استفاده از توابع بسل (Bessel Functions) نمایش داد.

این امکان، پایه ای برای درک ریاضیات مدولاسیون فرکانس در حوزه فرکانس (Frequency Domain) را فراهم می آورد.