کنترل تطبیقی مستقیم و غیرمستقیم

کنترل تطبیقی مستقیم و غیرمستقیم:
کنترل کننده تطبیقی از ترکیب یک تخمینگر پارامتر برخط (آنلاین)، که در هر لحظه پارامترهای نامعلوم را تخمین می زند و یک قانون کنترل با پارامتر معلوم تشکیل می شود.

تخمینگرِ پارامتر را که قانون تطبیق (Adaptive Law) نیز نامیده می شود، می توان به دو صورت با قانون کنترل ترکیب کرد.

در روش اول، که کنترل تطبیقی غیرمستقیم (Indirect Adaptive Control) نام دارد، پارامترهای دستگاه یا سیستم به صورت آنلاین تخمین زده شده و برای محاسبه پارامترهای کنترل کننده مورد استفاده قرار می گیرند.

این روش کنترل تطبیقی صریح (Explicit Adaptive Control) نیز نامیده می شود، زیرا طراحی براساس یک مدل صریح انجام می شود.

در روش دوم، که به کنترل تطبیقی مستقیم (Direct Adaptive Control) معروف است، مدل سیستم برحسب پارامترهای کنترل کننده به صورت پارامتری است و این پارامترها مستقیماً و بدون تخمین پارامترهای سیستم تحت کنترل تخمین زده می شوند.

از این روش با نام کنترل تطبیقی ضمنی (Implicit Adaptive Control) نیز یاد می شود، زیرا طراحی آن مبتنی بر تخمین مدل ضمنی سیستم است.

کنترل تطبیقی غیرمستقیم:
در کنترل تطبیقی غیرمستقیم، مدلP(θ∗) نسبت به بردار پارامتر مجهولθ∗ پارامتری می شود. برای مثال، در مدل یک سیستم خطی تغییرناپذیر با زمان (LTI) تک ورودی-تک خروجی (SISO)، θ∗ نشان دهنده ضرایب نامعلوم صورت و مخرج تابع تبدیل سیستم است.

یک تخمینگر پارامتر آنلاین تخمینθ(t) را ازθ∗در هر زمانtبا پردازش ورودی u و خروجی y سیستم تولید می کند.

تخمین پارامترθ(t) یک مدل تخمین زده شده را مشخص خواهد کرد که با^P(θ(t))نشان داده شده و در طراحی کنترل به عنوان مدل «صحیح» سیستم در نظر گرفته می شود و برای محاسبه پارامتر کنترل کننده یا بردار بهرهθc(t) با حل معادله جبری مشخصθc(t)=F(θ(t)) در زمان t مورد استفاده قرار می گیرد.

فرم قانون کنترلC(θc) و معادله جبریθc=F(θ) مشابه فرم قانون کنترلC(θ∗c) و معادلهθ∗c=F(θ∗) انتخاب می شود تا بتوان الزامات عملکرد مدل را برآورده کرد.

بنابراین، واضح است که با این روش، C(θc(t)) در هر لحظه به گونه ای طراحی می شود که الزامات عملکرد مدل تخمین زده شدهˆP(θ(t)) را که ممکن است نسبت به مدل نامعلومP(θ∗) متفاوت باشد، برآورده کند.

در نتیجه، مسئله اصلی در کنترل تطبیقی غیرمستقیم انتخاب دسته ای از قوانین کنترلC(θc) و دسته تخمینگرهای پارامتری θ(t) و معادله جبری θc(t)=F(θ(t))به گونه ای است که C(θc(t))الزامات عملکرد مدلP(θ∗) را با متغیر نامعلوم θ ∗ برآورده کند.

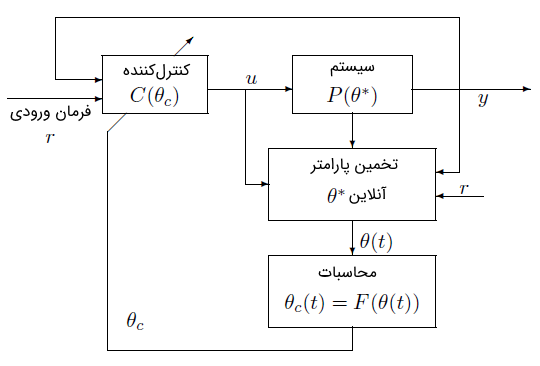
نمودار بلوکی طرح کنترل تطبیقی غیرمستقیم در شکل 4 نشان داده شده است.

کنترل تطبیقی مستقیم:
در کنترل تطبیقی مستقیم، مدلP(θ∗) برحسب بردار پارامترهای نامعلومθ∗c کنترل کننده، به گونه ای پارامتری می شود که کنترل کنندهC(θ∗c) الزامات عملکرد مدلPC(θ∗c) را با مشخصه دقیقاً مشابه با مشخصه ورودی-خروجیP(θ∗) برآورده سازد.

در این رویکرد کنترلی، تخمینگر آنلاین به جای P(θ∗) براساس Pc(θ∗c) طراحی شده است تا در هر لحظه، با پردازش ورودیuو خروجیyدستگاه، مستقیماً تخمین θc(t) را برای θ∗c مهیا کند.

پس از آن، برای به روزرسانی بردارθc پارامتر کنترل کننده، از تخمینθc(t) استفاده می شود.

مسئله اساسی کنترل تطبیقی مستقیم، انتخاب دسته قوانین کنترلC(θc) و تخمینگرهایθc(t) برای داشتن کنترل کنندهC(θc(t)) که موجب برآورده شدن الزامات عملکرد مدلP(θ∗) است.

ویژگی های مدلP(θ∗) در به دست آوردن مدل پارامتریPc(θ∗c) که تخمین آنلاین آن راحت باشد، بسیار مهم هستند.

در نتیجه، کنترل تطبیقی مستقیم به دسته های مشخصی از مدل ها محدود می شود. دسته ای از مدل ها که برای کنترل تطبیقی مستقیم مناسب هستند، شامل همه مدل های LTI و SISO می شوند که کمینه فاز باشند؛ یعنی صفرهای آن ها در سمت چپ محور موهومی صفحه مختلط واقع شده باشد.

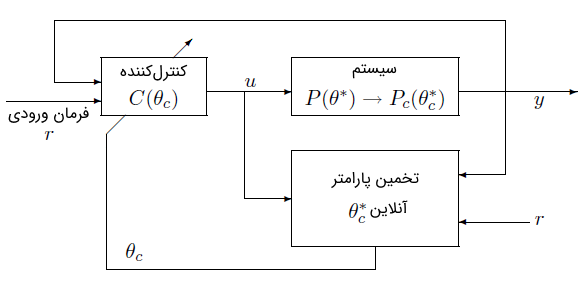
نمودار بلوکی کنترل تطبیقی مستقیم در شکل 5 نشان داده شده است.

قاعده اصلی در طراحی کنترل تطبیقی مستقیم و غیرمستقیم در شکل های 4 و 5 به صورت ساده نشان داده شد.

در طراحیC(θc)از تخمینθc(t) (در کنترل تطبیقی مستقیم) یا تخمینθ(t) (در کنترل تطبیقی غیرمستقیم) درست مانند مقادیر اصلی شان استفاده می کنیم.

این روش طراحی هم ارزی قطعیت (Certainty Equivalence) نام دارد و می توان از آن برای تولید دسته وسیعی از طرح های کنترل تطبیقی با ترکیب تخمین های آنلاین با قوانین کنترلی مختلف استفاده کرد.

ایده پشت این هم ارزی آن است که وقتی تخمین هایθc(t)وθ(t) به ترتیب به مقادیر واقعیθ∗cوθ∗ همگرا شوند، عملکرد کنترل کننده تطبیقی C(θc)به عملکردی میل کند که توسط C(θ∗c) برای پارامترهای معلوم به دست می آید.