نظریه آشوب (معادله لجستیک)

نظریه آشوب (معادله لجستیک):

معادله لجستیک که «مدل ورهاست» (Verhulst Model) نیز نام دارد، به صورت زیر است:

xn+1=rxn(1-xn)

که در آن، r پارامتری است که نرخ رشد را نشان می دهد و x n متغیر در تکرار n اُم و n متغیر اجرا است. این معادله، یک مدل رشد جمعیت است که که اولین بار توسط پییر فرانسوا ورهاست (Pierre François Verhulst) منتشر شد.

نسخه گسسته معادله لجستیک، به عنوان «نگاشت لجستیک» (Logistic Map) شناخته می شود.

نگاشت لجستیک، یک تصویر (Mapping) چندجمله ای است که اغلب به عنوان نمونه ای برای نشان دادن این موضوع به کار می رود که چگونه یک رفتار پیچیده آشوبی می تواند از معادلات دینامیکی غیرخطی ساده ناشی شود (تابعf در فضای فاز حالت بعدی z، یعنیf(z) (تصویر) را به دست می دهد.

این گفته را می توان به صورتz′=f(z) نوشت که در آن، علامت پریم به معنای نقطه بعدی است).

نگاشت لجستیک یک نگاشت وارون ناپذیر است؛ یعنی می توان آن را در زمان رو به جلو تکرار کرد و ازxnبه یکxn+1 رسید، اما عکس این عمل شدنی نیست. این نگاشت، تابع نگاشت تکرارشونده نیز نامیده می شود، زیرا یک مقدارxبه نامx0 را به مقدار دیگری از آن به نامx 1 می نگارد.

با انجام مداوم تکرارها نگاشت لجستیکی رفتارهای متنوعی را نشان خواهد داد. دنباله جواب های تکرارشونده یک مسیر یا مدار نامیده می شود.

نمودار انشعاب نگاشت لجستیک:
انشعاب یا دوشاخگی (Bifurcation)، یک تغییر کیفی در دینامیکی است که در اثر تغییر یک پارامتر سیستم رخ می دهد.

یک نمودار دوشاخگی، مقادیر طولانی مدت ممکن یک متغیر از یک سیستم را نشان می دهد که می توان آن را به عنوان تابعی از پارامتر سیستم به دست آورد.

یک مثال، نمودار انشعاب نگاشت لجستیک است. در این حالت، پارامترr روی محور افقی شکل نشان داده شده و محور عمودی تراکم مقادیر جمعیت دراز مدت مربوط به تابع لجستیک را نشان می دهد.

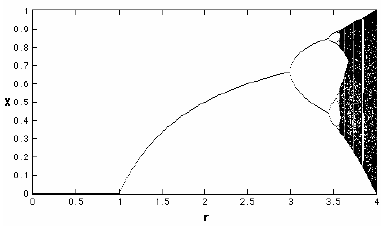
شکل بالا نشان می دهد که برایr های کوچک تر از 1، همه نقاط به صفر نگاشته می شوند. صفر جاذب یک نقطه برایr های کوچک تر از یک است.

برایr های بین 1 تا 3، هنوز جاذب های تک نقطه ای داریم. این مقدار جذب شدهx با افزایشr به حداقلr=3 افزایش می یابد.

انشعابات در r=3، r=3.45، r=3.54، r=3.564، r=3.569 و… تا زیر3.57 (که در آن، چند نوسان متناوب ناپایدار وجود دارد که همان رفتار آشوبی است) رخ می دهد.

یک تغییر کوچک درr ممکن است به یک سیستم آشوبی پایدار بسازد و برعکس. این دنباله، دو برابر شدن تناوب مسیر آشوب نام دارد.

دنباله دو برابر شدن دوره در طی انشعاب (جدا شدن به دو بخش) نقاط ثابت قبل (وقتی ناپایدار می شوند) رخ می دهد.

این موضوع به خوبی شکل گیری تناوب های ممکن چرخه های پایدار را از 1 به 2 به 4 به 8 و… نشان می دهد. این جدا شدن و بریدگی به عنوان «انشعاب چنگالی» (Pitchfork Bifurcation) شناخته می شود.

در هر نقطه انشعاب دو برابر دوره تناوب، نقطه ثابت دوره ای پایدار قبلی ناپایدار شده و دو نقطه ثابت پایدار ادغام می شوند.

این معادله مشخص می کند که چگونه سیستم های قطعی (خروجی های پایدار)، هنگامی که تحت فشار قرار می گیرند، می توانند خروجی های غیرقابل پیش بینی و آشوبی تولید کنند.

برای مقادیر بزرگ ترr (3.5تا4) سیستم وابستگی حساسی به شرایط اولیه نشان می دهد؛ یعنی تغییرات جزئی در مقدار r منجر به خروجی های بسیار متفاوتی خواهد شد.

یک ویژگی جالب این نمودار این است که وقتی تناوب به بی نهایت می رود، r محدود باقی می ماند. هنگامی که r بزرگ تر از تقریباً 3.57 باشد، مدارها (چرخه ها) آشوبی می شوند.

بنابراین، این نمودار انشعاب یک مثال خوب برای بیان اهمیت نظریه آشوب حتی در سیستم های غیرخطی بسیار ساده است.

نمودار انشعاب یک ابزار اساسی برای مطالعه تغییر رفتار سیستم در پاسخ به تغییرات پارامترهای سیستم است.