روش های شناسایی عیب (روش های مدل مبنای کمی)

روش های شناسایی عیب (روش های مدل مبنای کمی):
همان طور که اشاره کردیم، در یک دسته بندی کلی و رایج می توان انواع شناسایی را به روش های مدل مبنای کمی، مدل مبنای کیفی و بر مبنای تاریخچه فرایند تقسیم بندی کرد.

بیشتر اقدامات انجام شده در زمینه روش مدل مبنای کمی، بر اساس مدل‏ های عمومی ورودی- خروجی و فضای حالت هستند.

انواع مختلفی از مدل‏های کمی مانند مدل ‏های اصول اولیه، مدل های پاسخ فرکانسی در بحث تشخیص عیب استفاده شده‏ اند. مثلا در یک فرآیند مهندسی شیمی، برای تعیین مدل مولفه اولیه، تعادل های جرم، انرژی و ممنتوم و روابط اصلی (مانند معادلات حالت) در ارتقای معادلات مدل به کار می روند.

مدل های مولفه اولیه بر مبنای یک فهم فیزیکی از فرایند به دست می‏ آیند، اما به دلیل پیچیدگی محاسباتی در کاربرد بلادرنگ آن ها در سیستم های تشخیصی و نیز دشواری توسعه آن ها، چندان در تشخیص عیب مشهور نیستند. علاوه بر این، فرآیندهای مهندسی معمولا غیرخطی هستند که روند طراحی تشخیص عیب را دشوارتر می سازد.

اما به واسطه دسترسی به کامپیوترهای بهتر و سریع‏تر و فهم بهتر از طراحی و ترکیب کنترل‏ کننده ‏های غیرخطی، این وضعیت رو به بهبود است. بیشتر روش های تشخیص عیب بر مدل های جعبه سیاه مانند ورودی-خروجی و فضای حالت مبتنی هستند.

تفاوت اصلی بین مدل‏ های اصول اولیه و جعبه سیاه این است که در مدل اصول اولیه پارامترها مفاهیم فیزیکی مشخص دارند که می تواند در روند تشخیص یا طراحی کنترل کننده بسیار سودمند باشد.

در مدل سازی کمی با وجود این که سیستم های دینامیکی، فرآیندهایی پیوسته هستد، اما کلیه ابزارهای تشخیص عیب از داده های نمونه برداری شده استفاده می کنند و به همین دلیل فقط مدل های گسسته در نظر گرفته می شوند.

اما مفاهیم اساسی، به جز تحلیل های جزئی، به مدل‏ های پیوسته منتقل می شوند. بیشتر دیدگاه‏ های مدل-مبنا، سیستم را خطی فرض می کنند وکاربرد آن ها برای سیستم غیرخطی نیازمند یک خطی سازی مدل حول نقطه کار است.

در بسیاری موارد، مخصوصا هنگام تشخیص مقاوم عیوب، مدل‏ های بسیار دقیقی از فرآیند مورد نیاز هستند.

بنابراین، علاوه بر مدلسازی تئوری فرآیند، تخمین پارامتر زمان پیوسته فرآیند نیز نقشی اساسی ایفا می کند. با توجه به این‏که روش ‏ها مبتنی بر انحرافات نسبت به فرآیند عادی هستند، در نتیجه تعریف فرآیند عادی و دنبال کردن تغییرات عادی آن با روش های تخمین از اهمیت بالایی برخوردار هستند.

برای مقادیر تغییرات کوچک متغیرها، مدل‏ های خطی شده می توانند کافی باشند. اما در حالت کلی مدل ‏های غیرخطی باید اعمال شوند. استفاده از مدل دینامیک به جای مدل استاتیک اطلاعات بیشتری را در اختیار ما قرار می دهند و امکان آشکارسازی عیوب بیشتر و یا کوچک‏تر را نیز فراهم می کنند.

در چند دهه اخیر اکثر تحقیقات انجام شده در زمینه تشخیص عیب مبتنی بر افزونگی تحلیلی، بر مساله تولید مانده تمرکز نموده ‏اند. زیرا تولید یک مانده با طراحی خوب، فرآیند ارزیابی مانده را تسهیل خواهد نمود. در نتیجه بیشتر روش‏ ها از تکنیک های ساده آستانه، برای تصمیم‏ گیری بر اساس مانده ‏ها استفاده می‏ کنند.

یک نکته مهم در سیستم های مبتنی بر مانده، پیاده سازی تکنیک هایی برای بررسی مانده است تا از هشدار اشتباه جلوگیری به عمل آید.

زیرا بروز مانده می تواند در اثر نویز، شناسایی نادرست و یا یک عیب باشد. دو سیاست اصلی برای ارزیابی مانده وجود دارد، استفاده از آزمون های آماری و نیز مبنای استانداردها.

با اتکا بر یک مدل صریح از دستگاه تحت پایش، کلیه روش های تشخیص عیب مدل-مبنا (و بسیاری از روش های تشخیصی آماری) نیازمند دو مرحله هستند.

• در گام اول عدم تطابق بین رفتار واقعی و مورد انتظار تولید می ‏شود. این نوع تناقض ها، که مانده نیز نامیده می شوند، سیگنال های مصنوعی هستند که عیوب سیستم را بازتاب می ‏دهند.
• گام دوم انتخاب یک قانون تصمیم گیری برای تشخیص عیوب مختلف است.

همان طور که قبلا اشاره کردیم، دو نوع افزونگی وجود دارد، افزونگی سخت افزاری و افزونگی تحلیلی. افزونگی سخت افزاری نیازمند سنسورهای اضافه است و در کنترل سیستم های بحرانی- ایمنی مانند حامل‏ های هواپیمای فضایی و دستگاه های انرژی هسته ای استفاده می شود. البته کاربرد این روش با توجه به هزینه اضافه و فضای افزوده مورد نیاز محدود است.

از سوی دیگر، افزونگی تحلیلی (که افزونگی تابعی، ذاتی یا ساختگی نیز نامیده می شود.) از وابستگی تابعی بین متغیرهای فرآیند حاصل می شود و معمولا با مجموعه ‏ای از روابط جبری و زمانی بین حالت ها، ورودی ها و خروجی های سیستم به دست می آید. بسته به این که افزونگی چگونه انجام شود می توان افزونگی تحلیلی را به دو دسته مستقیم و زمانی تقسیم نمود.

یک افزونگی مستقیم، با روابط جبری بین اندازه گیری های سنسورهای مختلف انجام می شود. این روابط در محاسبه مقدار اندازه گیری یک سنسور از طریق اندازه گیری های دیگر سنسورها سودمند هستند. سپس مقدار محاسبه شده با مقدار اندازه‏ گیری شده از سنسور مقایسه می شود. وجود اختلاف، نشان می دهد که ممکن است یک عیب سنسور رخ داده باشد.

از طرف دیگر، یک افزونگی زمانی، از روابط دیفرانسیلی یا تفاضلی بین خروجی‏ های سنسورهای مختلف و ورودی های عملگرها به دست می آید. با داده ‏های ورودی و خروجی فرآیند، افزونگی زمانی برای آشکارسازی عیب حسگر و عملگر مناسب است. هرگونه تناقض که به صورت مانده ‏ها بیان می شود، می تواند برای اهداف آشکارسازی و جداسازی به کار رود.

هنگامی که هیچ عیبی رخ داده نداده است، مانده ها باید نزدیک به صفر باشند، اما هنگامی که سیستم اصلی تغییر می ‏کند، اندازه مانده ها مقادیر قابل توجهی را نشان می ‏دهند. مانده ‏ها باید نسبت به نویز، اغتشاش و عدم ‏قطعیت های مدل حساس نباشد و هم‏زمان بیشترین حساسیت را نسبت به عیوب داشته باشد.

در حالت ایده ال، مانده ها تنها وقتی غیر صفر هستند که عیبی رخ دهد. در این حالت انتخاب یک آستانه امری آسان است و یک آستانه کوچک مناسب خواهد بود. اما در واقع حضور نویز مانده (ناشی از اغتشاشات اندازه گیری، اغتشاشات فرآیند و عدم قطعیت های مدل) نیز باعث می شود که مانده غیرصفر باشد و منجر به هشدارهای نادرست می شود.

یکی از راه‏ های مشهور حل این مساله، روش جداسازی (دکوپله کردن) اغتشاش است. در این روش، کلیه عدم ‏قطعیت‏ ها به منظور دکوپله سازی تأثیر عیوب و ورودی‏ های ناشناخته به صورتی در نظر گرفته می شوند که بتوان بین آن‏ ها تفاوت قائل شد.

برای این کار از فیلترهایی استفاده می شود که با نام مشاهده گرهای ورودی ناشناخته یا UIO شناخته می شوند

در ساده ترین شکل، یک مانده برابر با مربع اختلاف مقدار واقعی خروجی حسگر y و مقدار تخمین آن از روی مدل، y∗ است.

در فیلتر کردن مانده، میانگین وزنی نمونه های مانده محاسبه شده قبلی (به عبارت دیگر فیلتر میانگین رو به جلو) برای تولید مانده نهایی استفاده می شود. در تصویر زیر مراحل آشکارسازی عیب مدل-مبنا نشان داده شده است.

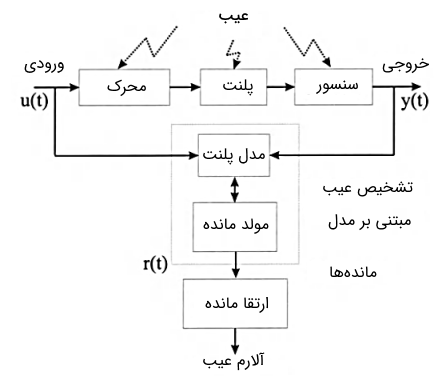
پس از آشکارسازی عیب، در مرحله بعد باید جداسازی عیب انجام شود. آشکارسازی عیب با یک سیگنال مانده امکان پذیر است، اما جداسازی عیب نیازمند مجموعه‏ ای از مانده‏ ها با عنوان بردار مانده است.

برای جداسازی عیب، تلاش هایی صورت گرفته است تا بتوان مولد مانده ‏هایی طراحی کرد که قابلیت تولید مانده های ارتقا یافته را داشته باشند. مانده های ارتقا یافته علاوه بر آشکارسازی عیب، منجر به جداسازی عیب نیز می شوند.

دو مورد از این روش های افزایشی، یعنی دیدگاه مانده جهت‏دار و دیدگاه مانده ساختاری، توجه بسیاری را به خود جلب نموده‏ اند. این اهمیت به دلیل توانایی این روش ها در تولید مانده‏ هایی است که خواص هدایتی یا ساختاری دارند و در نتیجه فرآیند جداسازی عیب را تسهیل می ‏کنند.

مولد‏های مانده ساختاری به گونه ‏ای طراحی شده‏ اند که هر مانده به صورت گزینشی به زیرمجموعه ‏ای از عیوب پاسخ می ‏دهد. این نوع طراحی امکان تشکیل نشانه‏ های عیب دودویی را برای جداسازی مرحله بعد فراهم می ‏کند. یعنی لازم است که تنها یک زیرمجموعه عیب خاص از اجزای مانده در پاسخ به یک عیب غیرصفر باشند.

در حالت تعادل، مانده ‏های متناظر با یک عیب خاص به یک زیرمجموعه از فضای کلی مانده منحصر می‏ شوند. مانده های ساختاری می توانند با معادلات توازن ساختاری در فرمت ARMA یا MA یا معادلات فضای حالت تولید شوند. هم چنین می توانند با استفاده از تخصیص ساختار ویژه مستقیم مشاهده ‏گر تشخیصی تولید شوند.

مولدهای مانده جهت‏دار قابلیت تولید مانده‏ هایی را دارند که به یک جهت خاص عیب در فضای چندبعدی مانده منحصر شده ‏اند. در نتیجه، مرحله جداسازی عیب، معادل تعیین یک جهت از پیش تعیین‏ شده است که مانده ‏ها به آن نزدیک‏تر هستند. طراحی یک مولد مانده جهت‏دار بر اساس سیستم های خطی نامتغیر با زمان با ابعاد محدود انجام می گیرد.

به مبحث شناسایی عیب در تحقیقات توجه کمتری شده است. اولین تلاش رسمی برای تخمین شدت عیوب توسط آیزرمن انجام شده است. در این کار فرض شده است که عیوب در پارامترهای فیزیکی سیستم نمود پیدا می کنند و با تخمین آنلاین آن ها می ‏توان شناسایی را انجام داد.

سه دسته روش برای تولد مانده وجود دارد:

• دسته اول، روش های مبتنی بر مشاهده گر (مبتنی بر فیلتر یا مبتنی بر تخمین حالت) نام دارند. این روش ها شامل یک بازسازی مبتنی بر مدل از خروجی های سیستم هستند و از اندازه گیری های حسگر (یا زیرمجموعه ای از اندازه گیری ها) و تعریف مانده ها به عنوان اختلاف بین اندازه گیری های واقعی و تخمین های مدل مبنا استفاده می کنند. به عنوان نمونه ای این از روش ها، می توان به مشاهده گرهای غیرخطی بهره بالا و فیلترهای کالمن اشاره کرد.
• دسته دوم، دیدگاه فضای توازن است که در آن مانده با استفاده از توابع توازن تعریف شده در یک پنجره زمانی از داده های ورودی و خروجی سیستم تولید می شود.
• دسته سوم، تخمین پارامتر است. این روش مبتنی بر این فرض است که عیوب در پارامترهای فیزیکی سیستم بازتاب داده می شوند. مانده ها در این روش برابر با اختلاف بین تخمین های برخط پارامترهای سیستم و مقادیر مربوطه در شرایط بدون عیب هستند. از روش های تخمین به کار رفته در این دسته می توان به UKF و شبکه عصبی تطبیقی اشاره کرد.

تخمین پارامتر:
اصلاح پارامتر برای تخصیص یک کمیت (عددی یا برداری) مورد استفاده قرار می گیرد که نامتغیر با زمان فرض می شود. اگر کمیت با زمان تغییر ‏کند، می ‏توان آن را یک پارامتر متغیر با زمان نامید، اما تغییرات زمانی آن باید در مقایسه با متغیرهای یک سیستم آهسته باشد.

تعیین انحرافات پارامترهایی که به صورت مستقیم اندازه گیری نشده اند، نیازمند روش های آنلاین تخمین پارامتر است و مدل ‏های پارامتری صحیح فرآیند، معمولا در حوزه پیوسته به شکل معادلات دیفرانسیلی معمولی و جزئی مورد نیاز هستند.

عیوبی که به صورت انحرافات پارامتری وابسته به زمان رخ می ‏دهند را می توان با روش های تخمین پارامتر مدیریت کرد. روش های تخمین پارامتر نیازمند در اختیار داشتن مدل های دینامیکی صحیح از فرآیند هستند و برای فرایندهای بزرگ حجم محاسباتی بالایی دارند. مهم‏ترین مقوله در استفاده از روش تخمین پارامتر برای تشخیص عیب، پیچیدگی است.

مدل فرآیند به کار رفته می تواند بر پایه داده ورودی-خروجی، مدل غیرخطی اصول اولیه یا یک مدل مرتبه کاهش یافته باشد.

در صورتی که مدل فرآیند، مدل پیچیده غیرخطی اصول اولیه باشد، مساله تخمین پارامتر به یک مساله بهینه‏ سازی غیرخطی تبدیل می شود.

در این صورت راه حل بلادرنگ مسائل بهینه ‏سازی غیرخطی پیچیده یک مشکل جدی در کاربرد این روش‏ ها است. مدل‏ های مرتبه کاهش یافته یا داده ورودی-خروجی در دیدگاه تخمین پارامتر قابل کاربرد است. لبته در این حالت قوام روش باید بررسی شود.

برای فرآیندهای تک ورودی- تک خروجی روش تخمین پارامتر به صورت خاص برای عیوب ضربی مناسب است، این روش آشکارسازی می تواند عمدتا برای عیوب مربوط به فرآیند و عیوبی توصیه شود که دینامیک عملگرها و حسگرها را تغییر می‏ دهند.

اما عیوب جمعی در ورودی و خروجی (مانند عیوب عملگر و حسگر استاتیک) نیز می توانند مشمول تخمین پارامتر شوند.

مشاهده ‏گر:
این روش مجموعه ‏ای از مشاهده ‏گرها را توسعه می ‏دهد که هر یک از آن ها به زیرمجموعه ای از عیوب حساس و به دیگر عیوب و ورودی‏ های ناشناخته غیرحساس هستند. درجات اضافی آزادی ناشی از اندازه ‏گیری و افزونگی مدل، امکان ایجاد این مشاهده گرها را فراهم می کنند.

ایده اصلی این است که در حالت بدون عیب، مشاهده‏ گرها فرآیند را به صورت دقیق دنبال می کنند و مانده ‏های ورودی‏ های ناشناخته، کوچک خواهند بود.

در صورتی که یک عیب رخ دهد، کلیه مشاهده گرهایی که توسط طراحی نسبت به این عیب غیرحساس شده اند، به ایجاد مانده های کوچک ادامه می دهند که این مانده ها تنها ورودی ‏های ناشناخته را انعکاس می ‏دهند. از سوی دیگر، مشاهده‏ گرهایی که نسبت به این عیب حساس هستند به صورت قابل توجهی از فرآیند منحرف شده و منجر به مانده هایی با اندازه بزرگ می شوند.

مجموعه مشاهده‏ گرها به صورتی طراحی می‏ شوند که مانده‏ های ناشی از آن‏ ها برای هر عیب، الگوی مانده متمایزی را تولید کنند.

این ویژگی جداسازی عیب را ممکن می‏ سازد. تولید سیگنال نشان دهنده عیب، با طراحی مشاهده‏ گرهایی تضمین می شود که جداسازی کامل عیوب را نشان می دهند و نسبت به اغتشاشات ناشناس غیرحساس هستند.

معادلات توازن:
«معادلات توازن» (Parity Equations)، گونه ‏های بازآرایی شده یا تبدیل‏ یافته از مدل‏ های ورودی- خروجی یا فضای حالت دستگاه هستند.

به صورت خلاصه می توان گفت که در روش معادلات توازن، سازگاری مدل ‏های دستگاه با خروجی های سنسور (اندازه‏ گیری‏ ها) و ورودی های معلوم فرآیند بررسی می شود. در شرایط کاری ایده ال و در حالت ماندگار، مانده بیان شده یا مقدار معادلات توازن صفر هستند.

ایده این دیدگاه بازآرایی ساختار مدل به گونه ‏ای است که بهترین جداسازی عیب صورت گیرد. روابط توازن دینامیکی توسط Willsky معرفی شد.

در طراحی معادلات تولید مانده افزونگی آزادی فراهم می‏ شود که بدین وسیله جداسازی عیب امکان ‏پذیر می شود. جداسازی عیب نیازمند تولید بردارهای مانده عمود بر هم برای عیوب مختلف است. هنگامی که اهداف طراحی تعیین شدند، معادله توازن و طراحی‏ های بر پایه مشاهده ‏گر منجر به مولدهای مانده یکسان یا معادل می ‏شوند.