کاربرد فیلتر تطبیقی در شناسایی سیستم

کاربرد فیلتر تطبیقی در شناسایی سیستم:
«شناسایی سیستم» (System Identification) یک روش برای مدلسازی سیستم های ناشناخته محسوب می شود. در این روش، سیستم ناشناخته به صورت موازی با فیلتر وفقی قرار می گیرد و هر دو سیستم را توسط یک سیگنال یکسان تحریک می کنند.

زمانی که مجموع مربعات خطا کمینه شود، آن گاه می توان گفت که فیلتر وفقی همان مدل مطلوب سیستم را نشان می دهد.

ساختاری که برای شناسایی سیستم وفقی مورد استفاده قرار می گیرد، در تصویر زیر نمایش داده شده است.

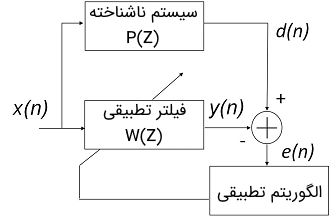
در این ساختار، P(z) برابر با سیستم ناشناخته است که قصد مدلسازی آن را داریم وW(z) نیز فیلتر وفقی مورد استفاده است.

این دو سیستم توسط سیگنالx(n) تحریک می شوند. همچنین سیگنال مطلوب d(n) خروجی سیستم ناشناخته است.

از طریق کمینه کردن خطای بینd(n) و y(n)، می توان مشخصه های سیستمP(z) را توصیف کرد.

خطای تخمین را می توان به صورت زیر نوشت:

در رابطه فوق، p(l) برابر با پاسخ ضربه سیستم ناشناخته است و با انتخاب هرw1(n) نزدیک بهp(l) مقدار خطا کاهش می یابد.

با استفاده از نویز سفید به عنوان سیگنال تحریک، کمینه سازیe(n) باعث نزدیک شدن سیگنالw1(n) به سیگنالp(l) می شود.

زمانی که اختلاف بین پاسخ سیستم فیزیکیdn) و پاسخ مدل وفقیy(n) کمینه شود، می توان گفت که مدل وفقی توانستهP(z) را از منظر ورودی خروجی تقریب بزند.

زمانی که پلنت مورد نظر متغیر با زمان باشد، الگوریتم وفقی نقش حفظ خطای مدلسازی در یک مقدار کوچک را دارد و این کار را به صورت تعقیب پیوسته تغیرات زمانی دینامیک پلنت انجام می دهد.

معمولا سیگنال ورودی، یک سیگنال با پهنای باند بزرگ است تا به فیلتر امکان داده شود که برای سیستم ناشناخته به یک مدل خوب دست یابد.

اگر سیگنال ورودی یک نویز سفید باشد، بهترین مدل برای سیستم ناشناخته، مدلی است که پاسخ ضربه آن با N+1 نمونه اولیه پاسخ ضربه سیستم ناشناخته همخوانی داشته باشد.

در مواردی که پاسخ ضربه سیستم ناشناخته دارای طول محدود و فیلتر وفقی از مرتبه مناسب باشد، به شرط این که نویز اندازه گیری یا نویز کانال وجود نداشته باشد، آن گاه مقدار معیار MSE برابر با صفر به دست می آید.

البته باید به این نکته توجه کرد که در کاربردهای عملی وجود نویز اندازه گیری غیر قابل اجتناب است.

در صورتی که این نویز با سیگنال ورودی وابستگی نداشته باشد یا به عبارت دیگر Uncorrelated باشند، آن گاه مقدار مورد انتظار برای ضرایب فیلتر وفقی با نمونه های پاسخ ضربه سیستم ناشناخته همخوانی خواهند داشت.

مشخص است که مقدار خطای خروجی با مقدار نویز اندازه گیری برابر خواهد بود. برخی از کاربردهای واقعی برای شناسایی سیستم وفقی در زمینه سیستم های کنترلی و نیز تحقیقات لرزه شناسی است.