فاکتور Q در فیلتر میان گذر اکتیو:
در مدار یک فیلتر میان گذر اکتیو، عرض کلی باند عبور واقعی بین دو نقطه فرکانس قطع−3dB پایین و نقطه فرکانس قطع−3dB بالا تعیین کننده فاکتور Q یا «فاکتور کیفیت» (Quality Factor) مدار فیلتر است.
توجه کنید که فاکتور کیفیت در یک فیلتر پایین گذر اکتیو معیاری است برای تعیین این که فیلتر نسبت به بازه فرکانسی ورودی به آن تا چه اندازه باند عبور گزینش گر یا «غیر گزینش گری» (Un-selective) دارد.
هرچه فاکتور Q در فیلتر پایین تر باشد، پهنای باند فیلتر میان گذر اکتیو پهن تر است و هر چه مقدار فاکتور Q بزرگ تر باشد، فیلتر میان گذر باند عبور باریک تری دارد و به عبارت دیگر، فیلتر میان گذر گزینشی تر عمل می کند.
فاکتور کیفیت یک فیلتر میان گذر را گاهی اوقات با حرف یونانیαنمایش می دهند و به آن «فرکانس پیک آلفا» (Alpha Peak Frequency) می گویند. رابطه بینα و فاکتور Q به صورت زیر نوشته می شود:
چون فاکتور کیفیت یک فیلتر میان گذر اکتیو (سیستم مرتبه دوم) به شیب پاسخ فرکانسی فیلتر در اطراف فرکانس نوسان مرکزی fr آن وابسته است، در نتیجه می توان فاکتور کیفیت را به صورت فاکتور میرایی یا «ضریب میرایی» (Damping Coefficient) نیز در نظر گرفت.
زیرا هر اندازه که فیلتر میرایی بالاتری داشته باشد، پاسخ فرکانسی آن مسطح تر است و هر اندازه که سیستم میرایی ضعیف تری داشته باشد، از مسطح بودن پاسخ فرکانسی نیز کاسته می شود و تیزتر می شود.
فاکتور ضریب میرایی را با نماد ξ نشان می دهند و بر اساس رابطه زیر محاسبه می کنند:
فاکتور Q مربوط به یک فیلتر میان گذر برابر با نسبت فرکانس رزونانس f r به پهنای باند بین فرکانس های −3dB بالا و پایین است. به این نکته توجه کنید که فاکتور کیفیت بدون واحد است:
در تصویر زیر ارتباط بین فاکتور کیفیت در فیلتر میان گذر اکتیو و پهنای باند آن نشان داده شده است.
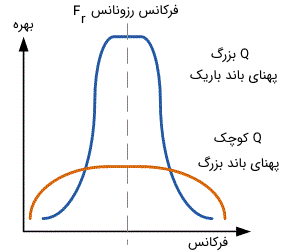
بنابراین برای فیلتر میان گذر اکتیو ساده مثال بخش های قبل، فاکتور کیفیت یا Q را می توان به طریق زیر محاسبه کرد:
هنگامی که عملکرد یک فیلتر میان گذر اکتیو را آنالیز می کنیم، معمولا یک فیلتر نرمال شده را در نظر می گیریم که پاسخ فرکانسی ایده آل تولید می کند.
پاسخ فرکانسی ایده آل به این صورت فرض می شود که شکل مستطیلی دارد و زمان انتقال بین باند عبور و باند توقف بسیار سریع و نیز شیب رول آف بسیار تند است.
اما نکته ای که وجود دارد این است که تولید پاسخ فرکانسی این چنین ایده آل در واقعیت و در مدارهای عملی امکان پذیر نیست.
بنابراین باید از تقریب استفاده کنیم تا بهترین پاسخ فرکانسی ممکن متناسب با فیلتری که در حال طراحی آن هستیم را در اختیار ما قرار دهد.
احتمالا بهترین و شناخته شده ترین تقریب فیلتر برای این کار، «فیلتر باترورث» (Butterworth) یا «فیلتر پاسخ مسطح بیشینه» (Maximally Flat Response Filter) است.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
