تعریف تاخیر سیستم ایده آل

تعریف تاخیر سیستم ایده آل:
یک سیستم می تواند به صورت ذاتی دارای «تاخیر» (Delay) باشد. تاخیر در یک سیستم کنترلی یا تاخیر سیستم را می توان به صورت واحدی در نظر گرفت که باعث به وجود آمدن یک شیفت زمانی در ورودی سیستم می شود.

اما تاخیر سیستم بر مشخصه های سیگنال ورودی تأثیر نمی گذارد. در این مطلب قصد داریم چگونگی نمایش تاخیر سیستم در حوزه لاپلاس را بررسی کنیم و بعد از نمایش تاخیر سیستم با تبدیل لاپلاس، به سادگی می توان با استفاده از تغییر متغیر، نمایش در سایر حوزه ها را نیز به دست آورد.

می توان گفت یک تاخیر سیستم ایده آل، تاخیری است که به هیچ وجه ویژگی های سیگنال را تغییر ندهد و فقط سیگنال را به اندازه یک زمان معین به تعویق بیندازد.

بعضی از تاخیرها، مانند «تاخیر پردازش» (Processing Delay) و «تاخیر انتقال» (Transmission Delay) غیرعمدی و غیر قابل اجتناب هستند.

سایر انواع تاخیر سیستم مانند «تاخیر سنکرون» (Synchronization Delay) یک بخش جامع از سیستم به حساب می آیند.

تاخیر سیستم ایده آل باعث می شود که تابع ورودی، در زمان به یک اندازه مشخص رو به جلو شیفت یابد. سیستم هایی که دارای تاخیر ایده آل هستند، باعث می شوند که خروجی آن ها به یک اندازه محدود و از پیش مشخص زمانی به تعویق بیفتد.

شیفت زمانی:
فرض کنید که یک تابع در حوزه زمان در اختیار ما قرار دارد که به اندازه یک مقدار زمانی ثابت و مشخص T در زمان شیفت یافته است.

برای راحتی می توان این تابع را با نماد x(t-T) نمایش داد. حال می توانیم نشان دهیم که تبدیل لاپلاس تابعx(t-T)به صورت زیر به دست خواهد آمد:

L{x(t-T)}⇔e-STX(S)

از رابطه بالا می توان نتیجه گرفت که شیفت زمانی یا تاخیر در حوزه زمان، به مقداری نمایی در حوزه مختلط لاپلاس تبدیل خواهد شد.

شیفت در حوزه Z:
یک تبدیل ستاره را در نظر می گیریم که بین تبدیل Z و تبدیل ستاره رابطه عمومی زیر وجود داشته باشد:

Z⇔eST

می توان نشان داد که یک شیفت زمانی برای مقادیر زمان گسسته، در حوزه Z به صورت زیر نشان داده خواهد شد:

x((n-ns)⋅T)≡x[n-ns]⇔z−nsX(z)

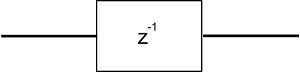
در تصویر زیر رابطه بین تاخیر به اندازه یک واحد و نمایش آن در حوزه تبدیل Z نشان داده شده است.