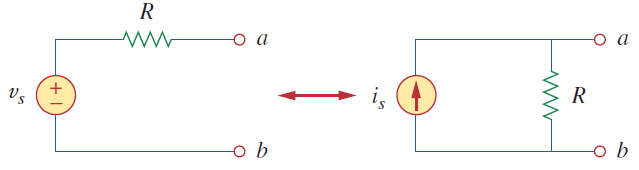تحلیل مدارهای الکتریکی چیست؟
تحلیل مدارهای الکتریکی معمولاً به فرایند مطالعه و تجزیه و تحلیل و محاسبه مقادیر مختلف الکتریکی مدار، به ویژه ولتاژها و جریان ها، گفته می شود.
در واقع، هرگاه جریان شاخه ها و ولتاژ گره های یک مدار را به دست آوریم، آن مدار را تحلیل کرده ایم.
برای حل مسائل مختلف تحلیل مدارهای الکتریکی، ابتدا باید واحدهای اساسی زیر را یاد بگیریم:
بسته به اندازه پیچیدگی مدار، از روش های مختلافی برای تحلیل مدار استفاده می شود. گاهی ممکن است تنها با قوانین ساده ای مانند قانون اهم تحلیل مدارهای الکتریکی را انجام داد. گاهی نیز پیچیدگی مدار به حدی است که باید از روش های پیشرفته تر استفاده کرد و محاسبات بیشتری را انجام داد. در ادامه، روش های مهم تحلیل مدارهای الکتریکی را معرفی می کنیم.
قانون اهم:
سال ها پیش، اهم، دانشمند آلمانی به این واقعیت پی برد که جریان گذرنده از یک مقاومت خطی در دمای ثابت، متناسب با ولتاژ دو سر آن است و رابطه عکس با مقدار مقاومت دارد. رابطه بین ولتاژ، جریان و مقاومت همان قانون اهم است که با رابطه زیر نشان داده می شود:
که در آن، V ولتاژ بر حسب ولت، I جریان برحسب آمپر و R مقاومت بر حسب اهم است. قانون اهم کاربرد گسترده ای در فرمول ها و محاسبات مهندسی برق و تحلیل مدار دارد.
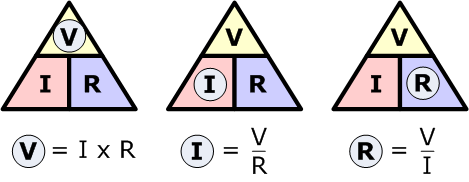
با دانستن دو مقدار از سه کمیت ولتاژ، جریان و مقاومت می توانیم با کمک قانون اهم مقدار کمیت سوم را بیابیم.
قوانین کیرشهف (KVL و KCL):
قوانین کیرشهرف (قانون جریان کیرشهف یا KCL و قانون ولتاژ کیرشهف یا KVL) از قوانین مهم و پایه ای تحلیل مدارهای الکتریکی هستند.
قانون جریان کیرشهف یا KCL بیان می کند که جریان یا بار الکتریکی وارد شده به یک گره از مدار الکتریکی دقیقاً برابر با بار یا جریانی است که از آن خارج می شود. به عبارت دیگر، مجموع جبری تمام جریان های وارد شده به یک گره باید برابر صفر باشد. این ایده کیرشهف، با نام پایستگی یا بقای بار نیز شناخته می شود.
قانون ولتاژ کیرشهف یا KVL بیان می کند که در هر شبکه حلقه بسته، کل ولتاژ حلقه برابر با مجموع تمام افت ولتاژهای موجود در آن است. به عبارت دیگر، مجموع تمام ولتاژهای حلقه باید برابر با صفر باشد. این ایده کیرشهف، به عنوان بقا یا پایستگی انرژی نیز شناخته می شود.
قضیه تونن:
قضیه تونن بیان می کند که هر مدار خطی متشکل از منابع ولتاژ و مقاومت ها را می توان با یک منبع ولتاژ با مقاومت سری با آن جایگزین کرد. به عبارت دیگر، می توان هر مدار الکتریکی را بدون توجه به میزان پیچیدگی، با یک مدار دو سر شامل منبع ولتاژ و مقاومت یا امپدانس سری با آن ساده کرد.
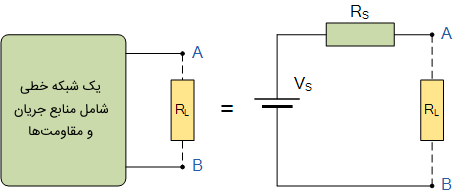
برای رسیدن به مدار معادل تونن، کارهای زیر را انجام می دهیم:
قضیه نورتن:
قضیه نورتن دوگان قضیه تونن است و بیان می کند: «هر مدار خطی از منابع انرژی و مقاومت ها را می توان به یک منبع جریان موازی با مقاومت کاهش داد. برای محاسبه منبع جریان معادل، دو سر مقاومت مورد نظر را اتصال کوتاه کرده و جریان گذرنده از آن را محاسبه می کنیم. توجه کنید که در این حالت، منابع در مدار حضور دارند.
تحلیل مش:
قوانین مداری کیرشهف ابزار اساسی تحلیل هر مدار پیچیده ای را به ما می دهند، اما راه های دیگری مانند روش تحلیل جریان مش و روش تحلیل ولتاژ گره وجود دارند که ریاضیات و محاسبات تحلیل شبکه های بزرگ را کاهش می دهند.
مِش در واقع ساده ترین حلقه در مدار است که شاخه ای درون آن وجود ندارد. به همین دلیل، مش فقط در مدارهای مسطح (یعنی مدارهایی که روی کاغذ بتوان رسم کرد بدون اینکه شاخه ها یکدیگر را قطع کنند مگر در گره ها) تعریف می شود.
تحلیل مش در گام های زیر انجام می شود:
تحلیل گره:
تحلیل گره، مکمل تحلیل مش است. این روش، ابزاری قدرتمند برای تحلیل مدارهای الکتریکی محسوب می شود و همان گونه از نام آن مشخص است، از معادلات قانون جریان کیرشهف (KCL) برای پیدا کردن ولتاژهای مدار استفاده می کند. در تحلیل گره، مدار با ولتاژ گره ها نسبت به یک گره مرجع (زمین) تحلیل می شود.
مراحل تحلیل مدار با روش تحلیل گره به صورت زیر است:
تبدیل منبع در مدار:
همان طور که می دانیم، معادلات ولتاژ گره (یا جریان مش) را می توان با تحلیل یک مدار، وقتی که منابع همه منبع جریان مستقل (یا ولتاژ مستقل) باشند، به دست آورد.
بنابراین، گاهی لازم است در تحلیل مدار، منبع ولتاژ سری با مقاومت را با منبع جریان موازی با مقاومت یا بالعکس جایگزین کنیم. هر کدام از این جایگزینی ها یک «تبدیل منبع» نامیده می شود.
قضیه جمع آثار:
اساس قضیه جمع آثار بر مشخصه خطی بودن استوار است. قضیه جمع آثار بیان می کند که ولتاژ یا جریان در عنصری از یک مدار خطی برابر با جمع جبری ولتاژ یا جریان آن عنصر است که از عملکرد هر کدام از منابع به تنهایی ناشی شده باشد. اصل جمع آثار از طریق محاسبه تأثیر هریک از منابع به صورت جداگانه به ما کمک می کند تا تحلیل یک مدار با بیش از یک منبع مستقل را آسان تر انجام دهیم.
برای اعمال قضیه جمع آثار باید به دو نکته توجه کنیم.
قضیه جمع آثار را می توان در سه گام اعمال کرد:
اما تحلیل مدارهای الکتریکی با استفاده از قضیه جمع آثار یک عیب بزرگ دارد. در اکثر موارد تحلیل مدار با استفاده از این روش ممکن است، زمان بیشتری طول بکشد. اگر مدار شامل سه منبع مستقل باشد، باید سه مدار ساده تر را هر بار برای محاسبه اثر یکی از منابع مستقل، آنالیز کنیم. با این حال قضیه جمع آثار در کاستن از پیچیدگی تحلیل یک مدار و تبدیل آن به مداری ساده تر، از طریق مدار باز کردن منابع جریان مستقل و اتصال کوتاه کردن منابع ولتاژ مستقل، بسیار مفید است.
لازم است به این نکته توجه کنیم که قضیه جمع آثار برای مدارات با مشخصه خطی صادق است و به همین دلیل برای محاسبه توان ناشی از هر منبع قابل اعمال نیست؛ زیرا توان جذب شده توسط مثلاً یک مقاومت به مربع جریان یا ولتاژ بستگی دارد. اگر به محاسبه توان یک المان نیاز داشته باشیم، باید ابتدا ولتاژ یا جریان آن المان را با قضیه جمع آثار محاسبه کنیم.
قضیه هم پاسخی:
قضیه هم پاسخی در تحلیل مدارهای الکتریکی برای منابع ولتاژ و جریان مستقل بیان می شود. در ادامه، این قضیه را برای منابع ولتاژ و جریان بیان می کنیم.
قضیه هم پاسخی برای منابع ولتاژ مستقل:
فرض کنید منبع ولتاژ مستقل یک مدار الکتریکی در شاخه nام آن جریان الکتریکی I را تولید کند (منظور از شاخه یک مسیر برای عبور جریان الکتریکی است). حال اگر محل منبع ولتاژ مستقل را تغییر دهیم به صورتی که از محل اولیه برداشته شده و به شاخه nام منتقل شود، آنگاه منبع ولتاژ مستقل (در محل جدید) در محل قبلی خود جریانی تولید می کند. این جریان برابر با جریان شاخه nام ناشی از منبع ولتاژ مستقل در محل قبلی است.
هنگام استفاده از قضیه هم پاسخی برای منبع ولتاژ مستقل گام های زیر طی می شود:
قضیه هم پاسخی برای منابع جریان مستقل:
فرض کنید منبع جریان مستقل یک مدار الکتریکی در گره nام آن ولتاژ الکتریکیV را تولید کند (منظور از گره محل اتصال مشترک دو یا چند المان مختلف مدار است). حال اگر محل منبع جریان مستقل را به گونه ای تغییر دهیم که از محل اولیه برداشته شده و به گره nاُم متصل شود، آنگاه منبع جریان مستقل (مستقر شده در محل جدید) در محل قبلی خود ولتاژی تولید می کند که دقیقا برابر با ولتاژV است.
این ولتاژ، همان ولتاژ گره nام ناشی از منبع جریان مستقل در محل قبلی است. هنگام اعمال این قضیه به مدارهای الکتریکی گام های زیر طی می شود:
قضیه تلگان در مدار:
«قضیه تلگان» در سال 1952 توسط مهندس برق هلندی، «برنارد دی اچ تلگان» (Bernard D.H. Tellegen) معرفی شد. این قضیه در تحلیل شبکه های الکتریکی بسیار مفید است. طبق قضیه تلگان، جمع توان های لحظه ای شاخه های یک شبکه الکتریکی صفر است. به عبارت دیگر، جمع انرژی تحویل داده شده به شاخه های هر شبکه الکتریکی در هر لحظه از زمان صفر است.
قضیه تلگان در طراحی فیلترها در پردازش سیگنال کاربرد فراوانی دارد و برای تنظیم پایداری در سیستم عامل های پیچیده نیز استفاده می شود. همچنین در سیستم های شیمیایی و بیولوژیکی و برای مشخص بررسی رفتار دینامیکی شبکه فیزیکی کاربرد دارد.
قضیه تلگان مستقل از عناصر شبکه است و برای تحلیل هر شبکه ای که از قانون جریان کیرشهف و قانون ولتاژ کیرشهف پیروی می کند، قابل اعمال است.
تحلیل حالت دائمی سینوسی:
تحلیل حالت دائمی سینوسی یکی از روش های مهم در تحلیل مدارهای الکتریکی AC است.
تحلیل مدارهای AC در سه گام اساسی انجام می شود:
توجه کنید که اگر مسئله خود در حوزه زمان مطرح شده باشد، از گام اول صرف نظر می شود. در گام دوم تحلیل مدار دقیقاً مانند آن چه در مدارهای DC انجام می شود، تکرار خواهد شد و تنها تفاوت در وجود اعداد مختلط در محاسبات حوزه فرکانس است.
کاربرد تبدیل لاپلاس در تحلیل مدارهای الکتریکی:
تبدیل لاپلاس، یک ابزار ریاضی قدرتمند برای تجزیه و تحلیل و طراحی است. توانایی بررسی مدارها و سیستم ها در حوزه فرکانس (s)، ما را در فهم بهتر عملکرد واقعی سیستم کمک می کند. علاوه بر این، می توانیم سیستم های فیزیکی را ساده تر و سریع تر بررسی کنیم.
استفاده از تبدیل لاپلاس در مدارهای الکتریکی، سه گام دارد:
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
