ولتاژ در مدارهای موازی

مدار موازی:
در این نوشتار در ابتدا سه اصل مهمی که در مورد مدارهای موازی برقرار است را بیان خواهیم کرد.

بر این اساس در یک مدار موازی همواره بین ولتاژ، جریان و مقاومت روابط زیر برقرار است:

• ولتاژ: در یک مدار موازی همواره ولتاژ دو سر اجزایی که به صورت موازی به یکدیگر متصل شده اند با هم برابر است.
• جریان: در یک مدار موازی جریان کل مدار برابر با مجموع جریان اجزایی از مدار است که به صورت موازی متصل شده اند.
• مقاومت: در یک مدار موازی که اجزای آن به صورت موازی متصل شده اند، مقدار مقاومت معادل از هر یک از مقاومت های منفرد کوچک تر است.

در ادامه چند نمونه از مدارهای موازی را بررسی می کنیم و تغییرات پارامترهای مختلف این مدارها را جستجو می کنیم.

همان طور که می دانید اجزای یک مدار را می توان به صورت متوالی یا سری، موازی یا ترکیبی از این دو به یکدیگر متصل کرد.

برای بحث در مورد مدارهای موازی با یک مدار موازی متشکل از سه مقاومت الکتریکی و یک باتری شروع می کنیم.

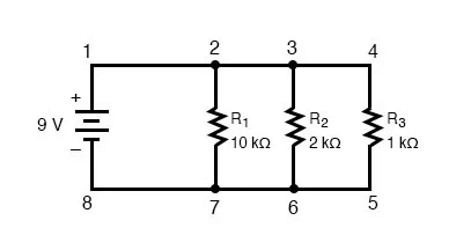
تصویر 1: مدار موازی متشکل از سه مقاومت و یک باتری

ولتاژ در مدارهای موازی:
اولین اصل مدارهای موازی این است که ولتاژ دو سر اجزایی از مدار که موازی با یکدیگر قرار گرفته اند با یکدیگر برابر است.

این ویژگی به این دلیل است که تنها دو نقطه مشترک الکتریکی در اجزای یک مدار الکتریکی موازی وجود دارد که مقدار آن ها باید در هر زمانی یکسان باشد.

بدین ترتیب در مدار داده شده در تصویر (1)، ولتاژ دو سر مقاومتR1 برابر با ولتاژ دو سر مقاومتR2 است، که این ولتاژ نیز برابر با ولتاژ دو سر مقاومتR3 اندازه گیری می شود. از این موضوع می توان نتیجه گرفت که ولتاژ دو سر هر یک از مقاومت های موازی برابر با ولتاژ دو سر باتری و 9 ولت است.

این موضوع در جدول زیر به خوبی نشان داده شده است:

کاربرد قانون اهم در یک مدار موازی ساده
مانند مدار متوالی قانون اهم برای مدار موازی نیز برقرار است و با دانستن مقدار ولتاژ، جریان و مقاومت در یک مدار می توان از قانون اهم استفاده کرد.

مشخص است که در مدار مورد بحث در تصویر (1) و با استفاده از جدول بالا به راحتی می توان قانون اهم را برای هر یک از مقاومت ها به کار برد و داریم:

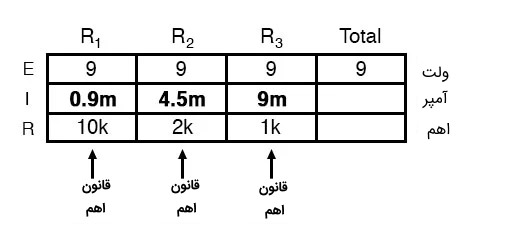
استفاده از قانون اهم در مدار موازی

در این مرحله هنوز مقدار مقاومت یا جریان را برای ستون آخر نمی دانیم و نمی توانیم از قانون اهم برای این ستون استفاده کنیم. اما اگر دقت کنیم می توانیم مقدار جریان را برای ستون آخر به دست آوریم، با توجه به اصل دوم گفته شده در مورد مدارهای موازی که جریان کل برابر با مجموع جریان دو سر هر قسمت از مدار است، می توانیم جریان کل را به دست آوریم.

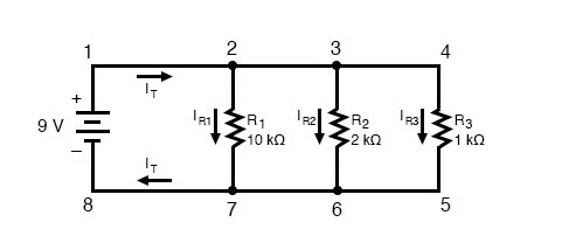
تصویر 2: جریان کل در مدار موازی
جریان خروجی از پایانه مثبت باتری در نقطه 2 دو شاخه می شود و مقداری از جریان از مقاومتR1 عبور می کند، این روند در نقطه 3 نیز تکرار می شود و جریان مجدداً به دو شاخه تبدیل می شود و جریان باقیمانده از جریان کل از مقاومتR3 عبور می کند.

جریان های عبوری از این مقاومت ها مجدداً در نقاط تقاطع مدار بعد از عبور از مقاومت هایR1، R2وR3 به هم می پیوندند و در نقطه 7 مدار، جریان خروجی از پایانه مثبت باتری به پایانه منفی باتری وارد می شود.

این همان اصل دوم مدارهای موازی است که جریان کل مدار برابر با مجموع جریان های عبوری از هر یک از اجزای مدار موازی است. با استفاده از این اصل جدول مدار ارائه شده در تصویر (1) به شکل زیر در می آید:

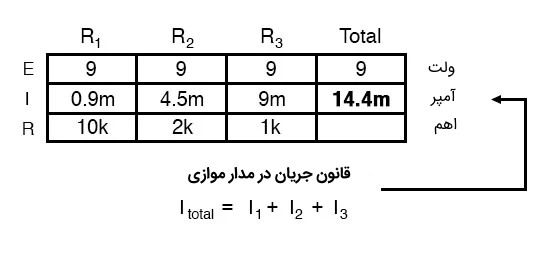
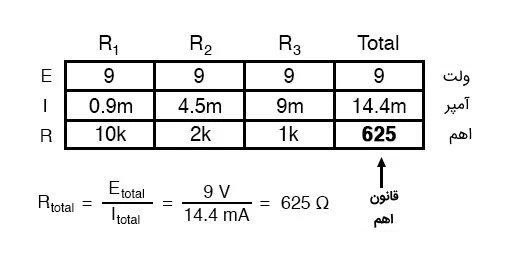
مقاومت کل در مدار موازی:
در نهایت با استفاده از قانون اهم می توانیم مقاومت کل را در یک مدار موازی محاسبه کنیم و داریم: