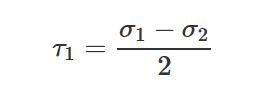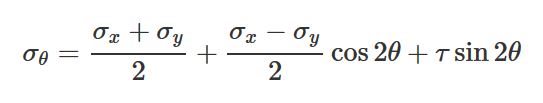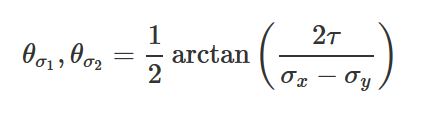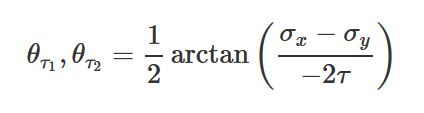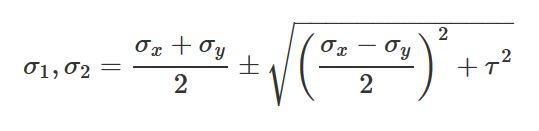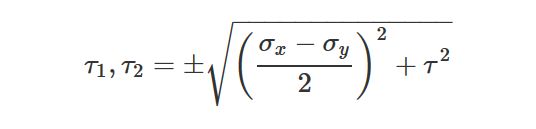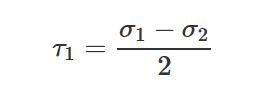آشنایی با تبدیلات تنش (مبانی مقاومت مصالح):
حالت کلی تنش در هر نقطه ای از یک جسم تحت بارگذاری را می توان با استفاده از سه تنش نرمال (یک تنش در هر راستا) و شش تنش برشی (دو تنش در هر راستا) نشان داد.
اندیس های موجود در کنار نام هر یک از تنش های نرمال (σ)، نشان دهنده راستای آن تنش در دستگاه مختصات است.
در کنار نام تنش های برشی نیز اندیس هایی وجود دارند؛ با این تفاوت که برخلاف نام گذاری در تنش های نرمال، این اندیس های تنش های برشی دارای دو مؤلفه هستند.
مؤلفه اول، راستای سطح عمود بر تنش و مؤلفه دوم، راستای تنش در دستگاه مختصات را مشخص می کند.
عموماً، تنش های موجود در یک راستا هنگامی صفر می شوند که حالت کلی تنش بر روی یک صفحه منفرد اعمال شده باشد (شکل زیر). به این حالت، تنش صفحه ای گفته می شود.
تنش صفحه ای، در صفحات نازک و همچنین سطوح خارجی تمام سازه های تحت بارگذاری رخ می دهد. از آنجایی که تنش خمشی و پیچشی، در سطح اجسام به حداکثر مقدار خود می رسند، تنش های صفحه ای معمولاً به عنوان مهم ترین تنش های موجود در محاسبات به حساب می آیند.
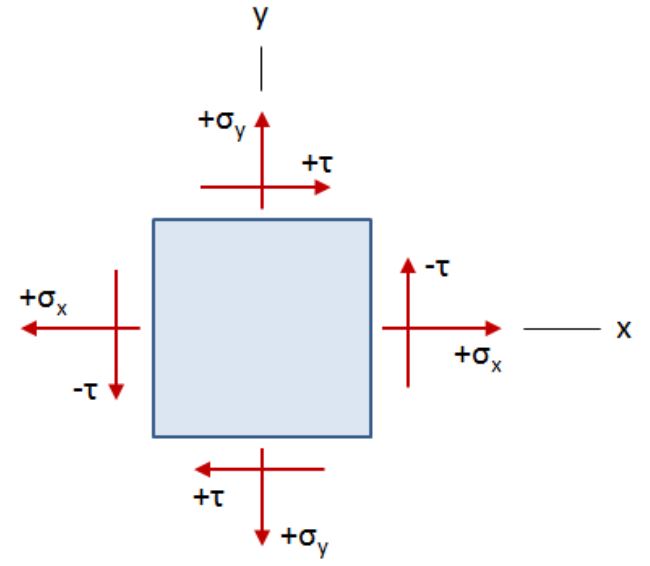
در شکل بالا، σx و σy، تنش های نرمال و τ، تنش برشی هستند. در این حالت، وضعیت تنش ها به گونه ای است که نقطه مورد نظر در حالت تعادل استاتیکی قرار داشته باشد.
از آنجایی که مقدار تمام تنش های برشی با هم برابر است، اندیس های آن ها به منظور ساده سازی حذف شده اند. با این وجود، توجه داشته باشید که علامت تنش های هم راستا با محور x، مثبت و تنش های هم راستا با محور y، منفی خواهد بود.
قواعد علامت گذاری صحیح، به گونه ای است که در شکل بالا نشان داده شده. برای تنش های نرمال، علامت تنش کششی، مثبت و علامت تنش فشاری، منفی در نظر گرفته می شود.
برای تنش های برشی، علامت تنش در جهت عقربه های ساعت، مثبت و برخلاف جهت عقربه های ساعت، منفی خواهد بود.
اگر مقدار تنش های نشان داده شده در شکل بالا مشخص باشد، می توان تنش های نرمال و برشی صفحه دوران یافته با زاویه θ (نسبت به افق) را تعیین کرد. با استفاده معادلات تبدیل در جدول زیر، مقادیر تنش های نرمال و برشی این صفحه دوران یافته به دست می آیند.
تنش نرمال:
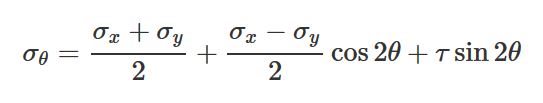
تنش برشی:
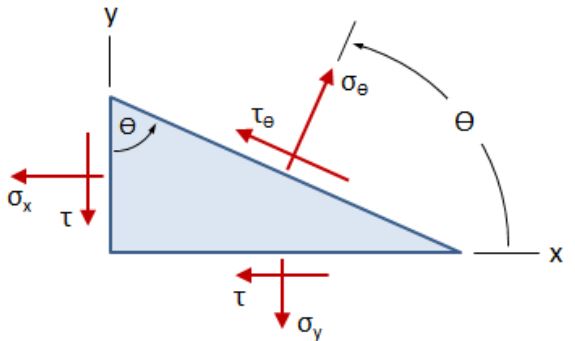
توجه داشته باشید که در شکل بالا، زاویه θ، نسب به محور x تعیین می شود. به علاوه، مقدار مثبت برای این زاویه، در جهت خلاف عقربه های ساعت است.
در هر نقطه از ماده، زوایایی را می توان یافت که تنش های نرمال و برشی صفحه در آن ها به مقادیر ماکسیمم و مینیمم خود می رسند. به تنش های نرمال ماکسیمم و مینیمم، تنش های اصلی گفته می شود. تنش های برشی ماکسیمم و مینیمم را نیز تنش های برشی حداکثری می گویند.
با مشتق گیری از معادلات تبدیل (نسبت به θ) و برابر قرار دادن آن ها با صفر، مقدار زوایای تنش های اصلی و برشی به صورت زیر به دست می آیند.
زوایای تنش اصلی:
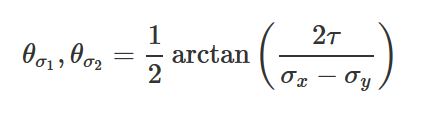
زوایای تنش برشی حداکثری:
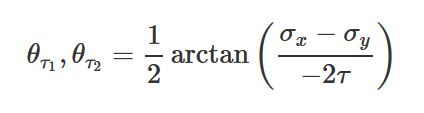
اگر زوایای بالا را در معادلات تبدیل جایگذاری کنیم، مقادیر تنش های اصلی و تنش های برشی حداکثری به صورت زیر خواهند بود:
تنش های اصلی:
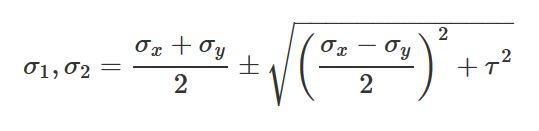
تنش های برشی حداکثری:
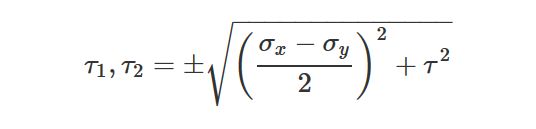
با بررسی معادلات مرتبط با تنش های اصلی و تنش های برشی حداکثری، می توان به نکات زیر پی برد:
معادلات زیر در محاسبات تنش های اصلی و حداکثری کاربرد زیادی دارند:
جمع تنش های نرمال، مقدار ثابتی است.
تنش برشی حداکثر، برابر است با نصف تفاضل تنش های اصلی.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
