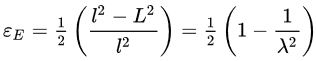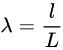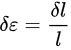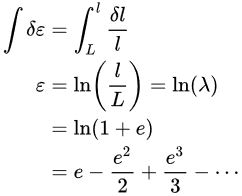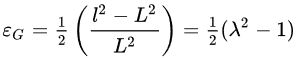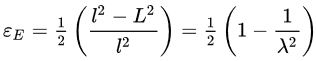تعاریف انواع کرنش در مواد:

بر اساس میزان کرنش یا تغییر شکل موضعی در یک جسم، تجزیه و تحلیل تغییر شکل را می توان به سه نظریه زیر تقسیم بندی کرد:
«نظریه تنش محدود» (Finite Strain Theory):
این نظریه با عناوینی همچون «نظریه کرنش بزرگ» (Large Strain Theory) و «نظریه تغییر شکل بزرگ» (Large Deformation Theory) نیز شناخته می شود و با تغییر شکل هایی سر و کار دارد که کرنش و چرخش در جسم مقدار بزرگی باشد.
در این وضعیت، تفاوت قابل توجهی بین پیکربندی های تغییر شکل یافته و بدون تغییر در جسم پیوسته وجود خواهد داشت و مرز بین این دو حالت کاملاً قابل تشخیص خواهد بود. این نظریه بیشتر برای مواد الاستومتر، موادی با تغییر شکل پلاستیک، سیالات و بافت های نرم بیولوژیکی کاربرد دارد.
«نظریه کرنش بی نهایت کوچک» (Infinitesimal Strain Theory):
این نظریه با عناوینی همچون «نظریه کرنش کوچک» (Small Strain Theory)، «نظریه تغییر شکل کوچک» (Small Deformation Theory) و «نظریه جابه جایی کوچک» (Small Displacement Theory) نیز شناخته می شود که در آن، کرنش و چرخش درون جسم مقدار کوچکی است.
در این شرایط می توان پیکربندی های تغییر شکل یافته و بدون تغییر را یکسان در نظر گرفت.
برای تجزیه و تحلیل تغییر شکل موادی با رفتار الاستیک از جمله فولاد و بتن که در مهندسی مکانیک و عمران به کار می روند، نظریه کرنش بی نهایت کوچک مورد استفاده قرار می گیرد.
«نظریه جابه جایی بزرگ» (Large- Displacement Theory):
این نظریه با عنوان «نظریه چرخش بزرگ» (Large-Rotation Theory) نیز شناخته می شود و در آن، تنش ها کوچک اما جابه جایی ها و چرخش ها کوچک هستند.
در هر یک از نظریه های بالا، کرنش به صورت متفاوتی تعریف می شود. مفهوم «کرنش مهندسی» (Engineering Strain)، رایج ترین مفهومی است که در حوزه مهندسی مکانیک و سازه مورد استفاده قرار می گیرد.
در حوزه های اشاره شده، مقدار تغییر شکل های مورد بررسی بسیار کوچک است. از سوی دیگر، برای موادی از قبیل الاستومرها و پلیمرها که در معرض تغییر شکل های بزرگ قرار دارند، مفهوم کرنش مهندسی (کرنش های مهندسی بالاتر از 1 درصد) قابل استفاده نیست.
در این موارد، از مفاهیم پیچیده تری مانند «کشش» (Stretch)، کرنش لگاریتمی، «کرنش گرین» (Green Strain) و «کرنش آلمانسی» (Almansi strain) استفاده می شود.
کرنش مهندسی:
«کرنش کوشی» (Cauchy strain) یا کرنش مهندسی به صورت نسبت تغییر شکل کل جسم تحت بارگذاری به ابعاد اولیه آن تعریف می شود.
برای المان های خطی مواد یا الیافی که به طور محوری تحت بارگذاری قرار گرفته اند، کرنش نرمال مهندسی (e) به صورت تغییرات طول (ΔL) نسبت به طول اولیه (L) آن المان های خطی یا الیاف تعریف می شود.
این کرنش را با عناوین دیگری از جمله «کرنش کششی مهندسی» (Engineering Extensional Strain) و «کرنش اسمی» (Nominal Strain) نیز معرفی می کنند.
در صورتی که الیاف ماده کشیده شوند، علامت کرنش نرمال مثبت و در صورت فشرده شدن این الیاف، علامت کرنش نرمال منفی خواهد بود.
به این ترتیب، کرنش نرمال را می توان با استفاده از رابطه زیر محاسبه کرد:
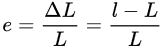
e: کرنش نرمال مهندسی؛ L: طول اولیه الیاف جسم؛ l: طول نهایی الیاف
توجه: اندازه گیری کرنش معمولاً به صورت بخش در میلیون یا میکروکرنش بیان می شود.
دو المان خطی در یک ماده را در نظر بگیرید که در پیکربندی اولیه (بدون تغییر شکل) به صورت عمود بر هم قرار گرفته اند. حال در صورت بررسی میزان تغییرات زاویه بین این دو المان، می توان کرنش برشی واقعی ماده را به دست آورد.
کرنش برشی مهندسی، به صورت تانژانت زاویه مذکور تعریف می شود و برابر است با طول تغییر شکل ماکسیمم تقسیم بر طول عمودی در صفحه ای که نیرو اعمال می شود. استفاده از این روش در برخی از مواقع محاسبات را ساده تر می کند.
در بخش های بعدی، توضیحات بیشتری را راجع به محاسبه کرنش نرمال و برشی ارائه خواهیم کرد.
نسبت کشش:
«نسبت کشش» (Stretch Ratio یا Extension Ratio)، معیاری برای اندازه گیری کرنش کششی یا نرمال یک المان خطی است که می تواند برای هر دو پیکربندی تغییر شکل یافته و بدون تغییر تعریف شود. این پارامتر، نسبت طول نهایی (l) به طول اولیه ماده (L) است.
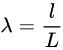
رابطه نسبت کشش با کرنش مهندسی به صورت زیر است:
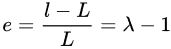
بر اساس معادله بالا، در صورتی که نسبت کشش برابر با یک باشد، کرنش نرمال صفر می شود و هیچ تغییر شکلی در ماده وجود نخواهد داشت.
نسبت کشش برای تجزیه و تحلیل موادی مانند الاستومترها به کار می رود که تغییر شکل های بزرگی را از خود به نمایش می گذارند و می توانند نسبتی بین 3 یا 4 را پیش از رسیدن به نقطه شکست خود تحمل کنند.
در طرف مقابل، شکست مواد رایج در مهندسی مکانیک و سازه (فولاد و بتن)، در نسبت های بسیار پایین تری رخ می دهد.
کرنش واقعی:
کرنش لگاریتمی (ε)، با عناوین دیگری مانند کرنش واقعی یا «کرنش هِنکی» (Hencky Strain) نیز شناخته می شود. یک کرنش تفاضلی مانند معادله زیر را در نظر بگیرید:
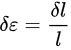
کرنش لگاریتمی را می توان با انتگرال گیری از این کرنش افزایشی (مانند معادله زیر) محاسبه کرد:
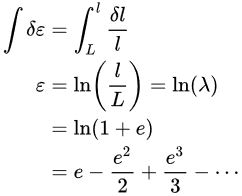
در معادله بالا، e، کرنش مهندسی است. هنگامی که یک سری کرنش تدریجی بر روی یک جسم اعمال می شود، کرنش لگاریتمی می تواند با در نظر گرفتن تأثیر مسیر کرنش، مقدار دقیق کرنش نهایی را محاسبه کند.
کرنش گرین:
«کرنش گرین» (Green Strain) به صورت معادله زیر تعریف می شود:
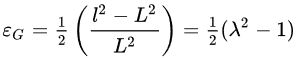
کرنش آلمانسی:
مقدار «کرنش اویلر-آلمانسی» (Euler-Almansi) را می توان با استفاده از رابطه زیر به دست آورد: