روش های تحلیل نیرو در خرپا

خرپا چیست؟
خرپا سازه ای چند عضوی است که تمامی بخش های آن به یکدیگر پین شده اند.

معنی پین این است که در هیچ مفصلی گشتاوری وجود ندارد؛ بنابراین در خرپا فقط نیرو وجود دارد. در شکل زیر می توانید یک خرپا و نیروهای خارجی وارد شده به آن را ببینید.

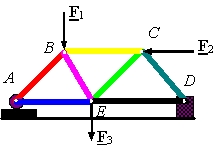
در حالت کلی به منظور تحلیل نیروهای موجود در یک خرپا از دو روش «مفاصل» (Joints) و «مقاطع» (Sections) استفاده می شود.

در هر خرپا با اعمال نیروی خارجی، درون هر عضو نیرویی ایجاد خواهد شد. برای مثال در خرپای شکل بالا که دو نیروی F2، F1 و F3 به آن وارد می شود، نیروهایی مطابق شکل زیر، در آن ایجاد شده است.

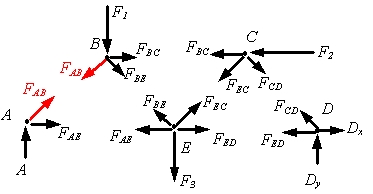
روش مفاصل:
در این روش هر مفصل را به صورت تنها تصور کنید؛ سپس برآیند تمامی نیروهای وارد شده به آن را صفر قرار دهید. بنابراین به منظور تحلیل نیرویی خرپا با استفاده از روش مفاصل، به ترتیب زیر عمل کنید:

• هر مفصل را به صورت جدا تصور کنید.
• نیروهای وارد شده به مفصل را معین کنید.
• برآیند نیروهای رسم شده روی مفصل را در راستای x و y برابر با صفر قرار دهید.

روش مقاطع:
در این روش بخشی از خرپا جدا شده و به عنوان سیستم در نظر گرفته می شود. سپس برآیند نیروها و گشتاورهای وارد شده به آن برابر با صفر قرار داده شده و نیروهای مجهول در مسئله به دست می آیند.

بنابراین برای به دست آوردن نیروهای مجهول موجود در یک خرپا به ترتیب زیر عمل کنید:

• انتخاب بخشی مناسب از خرپا به عنوان سیستم (این مفهوم در مثال های ارائه شده در پایین، به شکلی دقیق تر توضیح داده شده).
• قرار دادن تمامی نیروهای - خارجی - وارد شده به سیستم انتخاب شده.
• نوشتن معادله تعادل گشتاور و نیرو برای سیستم مفروض و محاسبه نیروهای مجهول قرار گرفته روی آن.

نکات کاربردی و مهم در تحلیل نیرویی خرپا:
توجه داشته باشید که همواره در تحلیل نیرویی خرپا، روش هایی میانبر وجود خواهند داشت. از این رو در این قسمت نکاتی مهم در مورد تحلیل نیرویی یک خرپا، در زمان کم تر را ارائه خواهیم داد.

1. اعضای خنثی در خرپا:
در یک خرپا ممکن است اعضایی وجود داشته باشند که نیرویی را حمل نکنند. این جمله به این معنی است که در عضو مد نظر نیرویی وجود ندارد.

در حقیقت می توان خرپا را بدون آن عضو تصور کرد. برای مثال در شکل زیر اعضایی که به رنگ آبی، قرمز و صورتی مشخص شده اند، نیرویی را در خود حس نمی کنند. [می توان تصور کرد که این اعضا در خرپا وجود ندارند.]

اجازه دهید مفهوم عضو خنثی را دقیق تر توضیح دهیم. در شکل بالا عضو B را بیرون کشیده و نیروهای وارد شده به مفصل را روی آن قرار می دهیم. در شکل زیر این کار انجام شده.

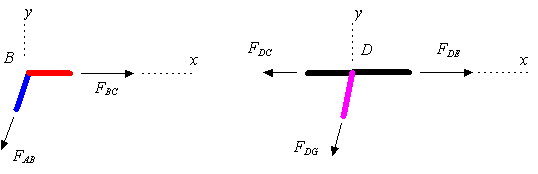
طبق مفاهیم بیان شده در مطلب مفاهیم استاتیک، بایستی برآیند نیروهای وارد شده به مفصل، در هر دو راستای x و y صفر باشد. بنابراین معادله تعادل نیرویی در راستای y برای این مفصل را می توان به صورت زیر نوشت.

∑ Fy=0→FABcos(theta)=0→FAB=0

2. نیروهای دو عضوی که در یک راستا قرار گرفته اند:
یک مفصل در خرپا ممکن است به شکلی قرار گیرد که فقط نیرو را از عضوی به عضو مقابل خود انتقال دهد. برای مثال در شکل زیر هیچ تغییری در نیروهای اطراف مفصل اتفاق نمی افتد و فقط نیرو در دو عضوی که در مقابل هم قرار دارند، منتقل می شود. برای نمونه در این خرپا روابط F1=F3 و F4=F2 برقرار هستند.

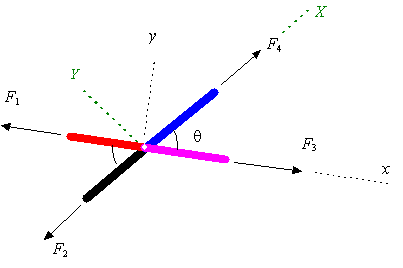
مثلا در این مفصل نیروهای F1 و F3 در راستای X قرار گرفته اند و به همین دلیل با هم برابر هستند.

3. خرپای معین و نامعین:
توجه داشته باشید که همواره به منظور تحلیل یک خرپا بایستی تعداد معادلات و تعداد نیروها با یکدیگر برابر باشند. برای بررسی این موضوع اجازه دهید چند نمونه را بررسی کنیم.

شکل زیر را در نظر بگیرید. می خواهیم تعداد نیروهای مجهول در این سازه و تعداد معادلاتی که می توان برای آن نوشت را مورد بررسی قرار دهیم. به نظر شما برای تحلیل این خرپا، چند نیروی مجهول وجود دارد.

نیروهای مجهول در شکل خرپای بالا:

Ay,FAE,FBE,FBC,FAB,FCD,FCE,FED,Dy,Dx

در حقیقت هر عضو یک نیرو را شامل می شود و 3 عکس العمل تکیه گاه در A و D [یک نیرو در A و دو نیرو در D] وجود دارند.

بنابراین کلا 10 نیرو بایستی محاسبه شود. هم چنین این خرپا از 5 مفصل تشکیل شده که در هرکدام از آن ها می توان 2 معادله تعادل نیرویی، در راستای x و y نوشت. در نتیجه می توان 10 معادله تعادل نیرویی، برای خرپا نوشت.

به طور خلاصه می توان گفت: 10 مجهول و 10 معادله برای این خرپا وجود دارد. به چنین سازه هایی، معین گفته می شود.

حال می خواهیم شما را به چالش بکشیم. بدین منظور خرپای زیر را در نظر بگیرید. به نظر شما در این خرپا چند نیرو وجود دارد؟ همچنین چند معادله می توان نوشت؟

نیروهای مجهول در این خرپا عبارتند از:

Ax,Ay,Dx,Dy,FAB,FAC,FBC,FCD,FDB

بنابراین 9 نیروی مجهول در این خرپا وجود دارد. هم چنین معادلاتی را که می توان برای این خرپا نوشت به شرح زیر هستند.

این خرپا از 4 مفصل تشکیل شده که بررای هرکدام از آن ها می توان دو معادله تعادلی∑Fx=0و∑Fy=0 را نوشت. بنابراین 8=2×4 معادله می توان برای این خرپا نوشت.

در نتیجه این خرپا دارای 9 مجهول است؛ در حالی که می توان 8 معادله برای آن نوشت. به خرپایی که تعداد معادلات آن از تعداد نیروهای مجهولش کمتر باشد، خرپای نامعین گفته می شود.

به منظور تحلیل نیرویی خرپای بالا، یکی از عضو های AC یا BD بایستی حذف شود [با این کار یک مجهول از معادلات کنار رفته و تعداد مجهولات و معادلات با هم برابر می شود].

4. مکانیزم:
در بالا به این نکته اشاره کردیم که اگر تعداد مجهولات در یک خرپا بیشتر از معادلاتش باشد، به آن نامعین گفته می شود و به منظور تحلیل نیرویی، بایستی یکی از عضوهای خرپا را حذف کرد.

حال شرایطی برعکس را تصور کنید. یعنی فرض کنید که در یک خرپا تعداد معادلات، از تعداد مجهولات بیشتر باشد. برای نمونه شکل زیر را تصور کنید.

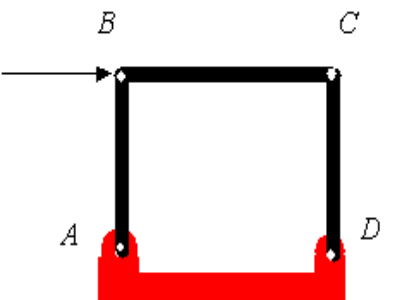
نیروهای مجهول در این سازه عبارتند از:

Ax,Ay,Dx,Dy,FAB,FBC,FCD

بنابراین این سازه دارای 7 نیروی مجهول است.

از طرفی این سازه دارای 4 مفصل است که برای هر کدام از آن ها می توان دو معادله تعادل، در راستای x و y نوشت؛ در نتیجه 8=2×4 معادله قابل بیان هستند.

بنابراین این سازه دارای 8 معادله و 7 مجهول است. جالب است چرا که تعداد معادلات از تعداد مجهولات بیشتر شده.

به سازه ای که در آن تعداد معادلات نیرویی از تعداد نیروهای مجهول بیشتر باشد، مکانیزم گفته می شود. چنین سازه ای قابلیت تحمل بارگذاری را نداشته و می تواند با گذشت زمان تغییر شکل دهد.