محدودیت های استفاده از رابطه تنش نرمال

محدودیت های استفاده از رابطه تنش نرمال:
کاربرد اصلی رابطه σ=P/A برای مواقعی است که تنش های موجود بر روی سطح مقطع میله دارای توزیع یکنواخت باشند.

تعریف_تنش2

این شرط زمانی تحقق می یابد که نیروی محوری P بر مرکز هندسی سطح مقطع اعمال شود. اگر نیروی P بر روی مرکز هندسی سطح مقطع اعمال نشود، میله با خمش مواجه خواهد شد.

در نتیجه، برای ارزیابی این شرایط به تحلیل های پیچیده تری نیاز خواهد بود. معمولاً در مسائل کاربردی فرض می شود که شرط بالا برقرار است؛ مگر اینکه خلاف آن در گزارش ها بیان شده باشد.

در شکل زیر، شرط یکنواخت بودن توزیع تنش برای تمام طول میله به جز انتهای آن صادق است. توزیع تنش در انتهای یک میله به نحوه انتقال بار P به درون آن بستگی دارد.

اگر این بار به صورت یکنواخت به انتهای میله وارد شود، الگوی تنش در این ناحیه با دیگر نواحی تفاوتی نخواهد داشت.

اگرچه، در صورت اعمال بار به صورت نقطه ای (از طریق یک میخ یا پیچ)، ناحیه ای با تجمع بالای تنش در انتهای میله به وجود می آید. به این ناحیه، «تمرکز تنش» (Stress Concentration) گفته می شود.

در شکل زیر، نمونه ای از یک نوع بارگذاری با احتمال وجود تمرکز تنش نمایش داده شده است. در این مثال، بارهای P به وسیله میخ های عبوری از حفره های انتهای میله به درون جسم اعمال می شوند.

نیروهای نمایش داده شده، برآیند فشارهای تکیه گاهی بین میخ و میله هستند. در این حالت، تمرکز تنش به وجود آمده در اطراف حفره های میله وضعیت پیچیده ای دارد.

اگرچه، با فاصله گرفتن از انتهای میله و حرکت به سمت مرکز آن، توزیع تنش به طور تدریجی یکنواخت می شود.

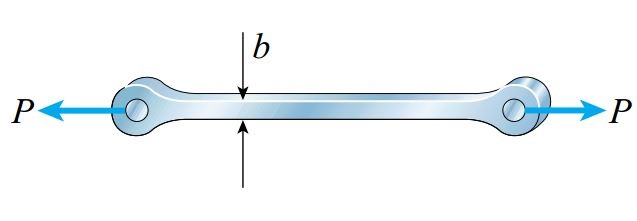
میله فولادی تحت بارگذاری کششی در محل قرارگیری میخ‌ها

به عنوان یک قانون کاربردی به خاطر داشته باشید که به کارگیری رابطه σ=P/A برای نقاط درون یک میله منشوری در صورتی از دقت خوبی برخوردار خواهد بود که این نقاط از محل تمرکز تنش به اندازه کافی (در امتداد بزرگ ترین بعد میله) فاصله داشته باشند.

به عبارت دیگر، توزیع تنش در مثال بالا برای فاصله b یا فواصل بیشتر از b یکنواخت است. b با عرض میله برابری می کند.

در شکل زیر، توزیع تنش برای فاصله d یا فواصل بیشتر از d نسبت به دو انتهای میله به صورت یکنواخت خواهد بود. d با قطر میله برابر است.

توجه: لازم به ذکر است که رابطه σ=P/A در هنگام غیر یکنواخت بودن توزیع تنش نیز قابل استفاده است زیرا این رابطه، مقدار تنش نرمال میانگین بر روی سطح مقطع را تعیین می کند.