انرژی کرنشی در میله های غیر یکنواخت

انرژی کرنشی در میله های غیر یکنواخت:

میزان انرژی کرنشی کل در میله های چندبخشی از حاصل جمع انرژی کرنشی هر بخش به دست می آید. شکل زیر را به عنوان یک مثال در نظر بگیرید. انرژی کرنشی این میله با جمع انرژی کرنشی در بخش های AB و BC برابر است.

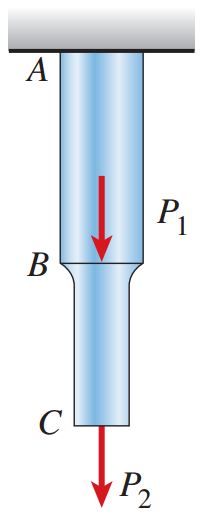
میله ای با دو بخش منشوری که تحت نیروهای محوری قرار گرفته است. مساحت سطح مقطع هر بخش با بخش دیگر متفاوت است.

رابطه ریاضی این مفهوم (برای رفتار خطی و غیر خطی) به صورت زیر بیان می شود:

U: انرژی کرنشی کل؛ Ui: انرژی کرنشی بخش i ام؛ n: تعداد بخش های میله

اکنون فرض کنید که ماده تشکیل دهنده میله دارای رفتار الاستیک خطی بوده و مقدار نیروی محوری در درون هر بخش ثابت است.

با در نظر گرفتن این فرض و قرار دادن رابطه انرژی کرنشی یک میله الاستیک خطی در فرمول بالا می توانیم انرژی کرنشی بخش های مختلف میله را محاسبه کنیم:

Ni: نیروی محوری اعمال شده بر بخش i ام؛ Li: طول بخش i ام؛ Ei: مدول الاستیسیته بخش i ام؛ Ai: مساحت سطح مقطع بخش i ام

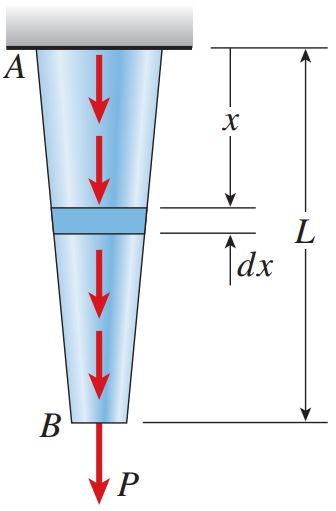
شکل زیر، نمونه ای از یک میله غیر منشوری را نمایش می دهد که در معرض یک نیروی محوری با تغییرات پیوسته قرار گرفته است.

برای تعیین انرژی کرنشی در این حالت می توانیم رابطه بالا را به فرم دیفرانسیلی تبدیل کنیم و سپس نسبت به تغییرات طول میله از آن انتگرال بگیریم:

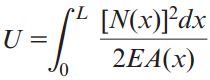
(N(x: نیروی محوری در فاصله x از انتهای میله؛ (A(x: مساحت سطح مقطع در فاصله x از انتهای میله