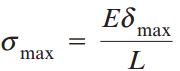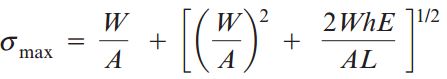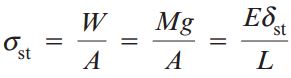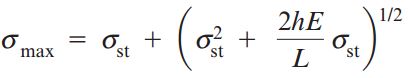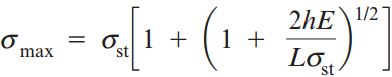تنش ماکسیمم در سازه

تنش ماکسیمم در سازه:
مقدار تنش ماکسیمم (σmax) در بارگذاری ضربه ای را می توان با استفاده از تغییر طول ماکسیمم به سادگی محاسبه کرد.

به این ترتیب، بر اساس فرض یکنواخت بودن توزیع تنش در طول میله داریم:

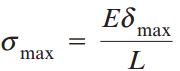
با جایگذاری رابطه بالا در رابطه تغییر طول ماکسیمم خواهیم داشت:

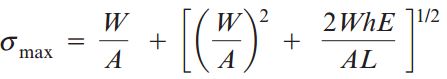
رابطه بالا را می توانیم برای شرایط بارگذاری استاتیک بازنویسی کنیم:

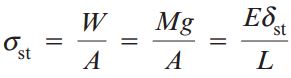
σst: تنش به وجود آمده در هنگام اعمال بار استاتیک

به این ترتیب، روابط تنش ماکسیمم به صورت زیر خواهد بود:

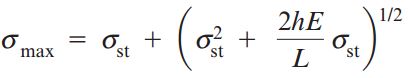
یا

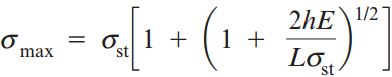
این رابطه نیز مانند رابطه δmax نشان می دهد که در صورت اعمال بارهای برابر، تأثیر بارگذاری ضربه ای بر روی میزان تنش های به وجود آمده بسیار بیشتر از تأثیر بارگذاری استاتیک است. اگر ارتفاع h نسبت به میزان کشیدگی میله بزرگ باشد، می توانیم مقادیر 1 را از درون معادله بالا حذف کنیم:

بر اساس این رابطه، افزایش انرژی جنبشی (Mv2/2) باعث افزایش میزان تنش و افزایش حجم میله (AL) باعث کاهش میزان تنش می شود.

به این ترتیب، در بارگذاری ضربه ای بر خلاف بارگذاری استاتیک، میزان تنش به طول میله (L) و مدول الاستیسیته (E) نیز بستگی دارد.

معادلات ارائه شده برای δmax و σmax تنها برای لحظه رسیدن فلنج به پایین ترین موقعیت قابل استفاده هستند.

پس از رسیدن به تغییر طول ماکسیمم، میله در راستای محور خود می لرزد.

این ارزش تا ثابت شدن میله در تغییر طول استاتیک ادامه می یابد. از این لحظه به بعد، مقادیر تنش و تغییر طول میله را می توان با استفاده از روابط δmax و σmax محاسبه کرد.

با وجود تعیین روابط δmax و σmax برای یک میله منشوری، این روابط برای تمام سازه های الاستیک خطی در شرایط بارگذاری ضربه ای قابل استفاده هستند.

به منظور، باید به جای عبارت EA/L در روابط مذکور از مقدار سختی سازه مورد تحلیل استفاده کرد.