تعریف معادلات تبدیل تنش صفحه ای

تعریف معادلات تبدیل تنش صفحه ای:
با استفاده از روابط مثلثاتی می توان معادلات تنش های اعمال شده بر روی مقطع دوران یافته را به صورت ساده تر بیان کرد.

به این منظور، در بخش زیر برخی از روابط مورد نیاز برای ساده سازی معادلات تنش ها آورده شده است:

با جایگذاری روابط بالا در معادلات تنش های اعمال شده بر مقاطع دوران یافته، خواهیم داشت:

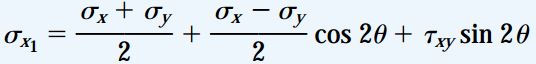
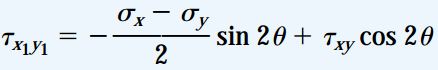
از آنجایی که این معادلات، مؤلفه های تنش را از یک دستگاه مختصات به دستگاه دیگر تبدیل می کنند، به آن ها معادلات تبدیل تنش صفحه ای گفته می شود.

اگرچه، حالت ذاتی تنش در نقطه مورد بررسی همیشه یکسان است و به دستگاه مختصات مورد استفاده برای نمایش تنش های اعمال شده بر روی المان بستگی ندارد.

معادلات تبدیل تنها از معادلات تعادل المان به دست می آیند. به همین دلیل، این معادلات برای تعیین تنش های اعمال شده بر روی تمام مواد (خطی یا غیرخطی، الاستیک یا غیر الاستیک) مناسب هستند.

در معادلات تبدیل می توان نکته مهمی را در مورد تنش های نرمال مشاهده کرد. در بخش قبلی دیدیم که با جایگذاری θ+90 به جای θ، تنش نرمال σy1 بر روی صفحه y1 در المان دوران یافته تعیین می شود.

به این ترتیب، معادله زیر برای محاسبه σy1 به دست می آید:

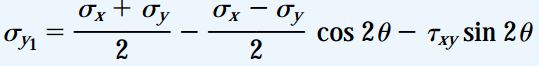
با جمع کردن σx1 و σy1، رابطه زیر برای تنش صفحه ای حاصل می شود:

رابطه بالا نشان می دهد که حاصل جمع تنش های نرمال اعمال شده بر روی صفحات عمود بر هم در المان های تنش صفحه ای، مقداری ثابت است و به زاویه θ بستگی ندارد.

شکل زیر، نحوه تغییرات تنش های نرمال و برشی را به صورت نمودار σx1 یا ?x1y1 در مقابل زاویه θ نمایش می دهد.

این نمودار برای حالت σy=0.2σx و ?yx=0.8σx رسم شده است. همان طور مشاهده می شود، با تغییر جهت المان، مقدار تنش ها نیز به طور پیوسته تغییر می کنند.

در زوایای خاص، تنش نرمال به یک مقدار حداکثری یا حداقلی می رسد. در برخی از زوایا نیز این تنش برابر با صفر می شود. این شرایط برای تنش برشی نیز صادق است.