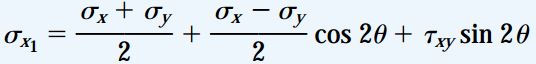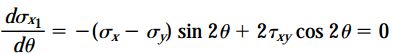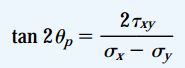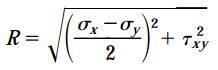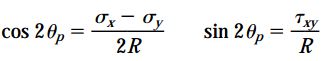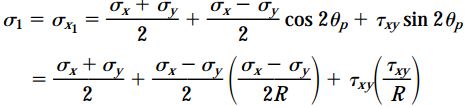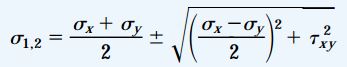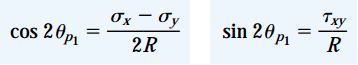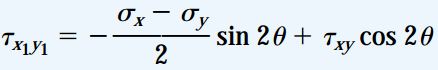تنش اصلی و تنش برشی ماکسیمم

تنش اصلی و تنش برشی ماکسیمم:
بر اساس معادلات تبدیل تنش صفحه ای، دوران محورها تحت زاویه θ باعث تغییر پیوسته تنش های نرمال σx1 و تنش های برشی τx1y1 می شود.

در شکل زیر، نمونه ای از تغییر تنش های نرمال و برشی با توجه به تغییر زاویه θ نمایش داده شده است. با توجه به این شکل، تنش های نرمال و برشی در هر 90 درجه به میزان ماکسیمم و مینیمم خود می رسند.

مشخصاً این مقادیر ماکسیمم و مینیمم در حین فرآیندهای طراحی و تحلیل سازه مورد استفاده قرار می گیرند.

به عنوان مثال، شکست ناشی از خستگی در سازه ها معمولاً به دلیل اعمال تنش های ماکسیمم رخ می دهد.

به همین دلیل، تعیین مقدار و جهت گیری این تنش ها به عنوان یکی از مهم ترین مراحل طراحی سازه مد نظر قرار می گیرد.

تنش های اصلی:
تنش های نرمال ماکسیمم و مینیمم با عنوان «تنش های اصلی» (Principal Stresses) شناخته می شوند. مقادیر این تنش ها با استفاده از معادله تبدیل زیر مورد محاسبه قرار می گیرند:

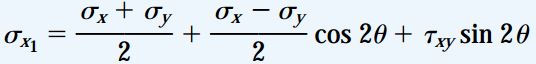
با مشتق گیری از σx1 نسبت به θ و برابر قرار دادن عبارت به دست آمده با صفر، معادله زیر حاصل می شود. با حل این معادله نسبت به θ، زوایایی به دست می آید که σx1 در آن ها دارای مقادیر ماکسیمم و مینیمم است.

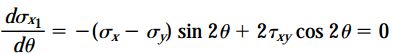
با استفاده از روابط مثلثاتی می توانیم رابطه تعیین زوایای 2θp را به صورت زیر بیان کنیم:

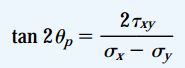
اندیس p در زاویه θp معرف جهت گیری صفحاتی است که تنش های اصلی بر روی آن ها قرار دارند و به آن ها «صفحات اصلی» (Principal Planes) گفته می شود.

با استفاده از رابطه بالا و در محدوده 0 تا 360 درجه، دو مقدار برای زاویه 2θp به دست می آید که یکی از آن ها در محدوده 0 تا 180 و دیگری در محدوده 180 تا 360 قرار دارد.

اختلاف بین این مقادیر 180 درجه است. به این ترتیب، یکی از مقادیر θp در محدوده 0 تا 90 و دیگری در محدوده 90 تا 180 قرار خواهد داشت و اختلاف بین آن ها 90 درجه خواهد بود.

در یکی از این زوایا، تنش نرمال σx1 به عنوان «تنش اصلی ماکسیمم» (Maximum Principal Stress) و در زاویه دیگر، تنش نرمال σx1 به عنوان «تنش اصلی مینیمم» (Minimum Principal Stress) در نظر گرفته می شود.

با قرار دادن مقادیر θp در اولین معادله تبدیل و حل کردن معادله نسبت به σx1، تنش های اصلی به دست می آیند.

در این روش نه تنها مقادیر تنش های اصلی بلکه زوایای مربوط به هر یک نیز مشخص می شوند. علاوه بر روش بالا می توان از چند فرمول کلی نیز برای محاسبه تنش های اصلی استفاده کرد.

برای آشنایی با این روش، مثلث نمایش داده شده در شکل زیر را در نظر بگیرید. این مثلث بر اساس رابطه تعیین زوایای 2θp ترسیم شده است.

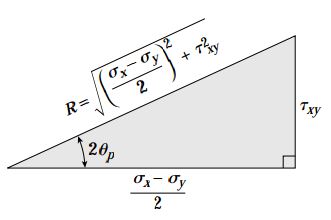
طبق نظریه فیثاغورس، طول وتر مثلث بالا برابر است با:

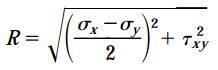
کمیت R در این رابطه دارای مقداری مثبت است. این کمیت با واحد تنش بیان می شود. بر اساس نظریه فیثاغورس می توان به دو رابطه زیر نیز دست یافت:

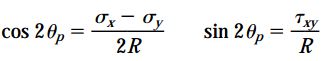
با بازنویسی رابطه σx1 بر اساس cos2θp و sin2θp، رابطه زیر برای تعیین تنش اصلی ماکسیمم (σ1) به دست می آید:

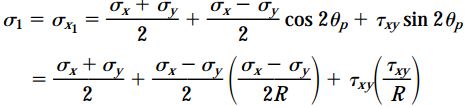
با جایگذاری رابطه کمیت R، معادله σ1 به فرم زیر تبدیل می شود:

به عنوان یک نکته مهم در نظر داشته باشید که جمع تنش های نرمال موجود بر روی صفحات عمود بر هم مقداری ثابت است:

به این ترتیب، با جایگذاری رابطه σ1 در معادله بالا، رابطه تنش اصلی مینیمم (σ2) نیز به دست می آید:

فرم رابطه بالا مشابه رابطه σ1 است؛ با این تفاوت که به جای علامت مثبت بین دو عبارت سمت راست در رابطه σ1، یک علامت منفی بین دو عبارت سمت راست رابطه σ2 وجود دارد.

با ترکیب روابط معرفی شده برای σ1 و σ2، یک رابطه کلی برای تعیین تنش های اصلی به دست می آید:

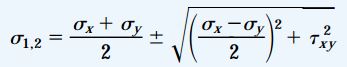
در این رابطه کلی، با به کارگیری علامت مثبت، تنش اصلی ماکسیمم (σ1) و با به کارگیری علامت منفی، تنش اصلی مینیمم (σ2) محاسبه می شود.

زوایای اصلی:
در این بخش به بررسی صفحات دربرگیرنده تنش های اصلی و زوایای معرف آن ها می پردازیم. مقادیر زوایای اصلی با استفاده از روابط tan2θp قابل محاسبه هستند. با این وجود، تفاوت بین θp1 و θp2 در این روابط مشخص نمی شود.

یک روش ساده برای تعیین زاویه اصلی ماکسیمم یا مینیمم، جایگذاری مقدار یکی از زوایا در رابطه σx1 و مقایسه آن با تنش های اصلی به دست آمده از رابطه کلی σ1,2 است.

اگر مقدار σx1 با σ1 برابر باشد، زاویه به کار گرفته شده به عنوان زاویه اصلی ماکسیمم و اگر مقدار σx1 با σ2 برابر باشد، زاویه به کار گرفته شده به عنوان زاویه اصلی مینیمم در نظر گرفته خواهد شد.

یک روش دیگر برای تشخیص زوایای اصلی ماکسیمم و مینیمم، استفاده از روابط cos2θp و sin2θp است. توجه داشته باشید که تنها زاویه θp1 در روابط مذکور صدق می کند. به این ترتیب می توانیم این روابط را به صورت زیر بازنویسی کنیم:

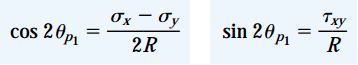
در محدوده 0 تا 360 درجه، تنها یک زاویه وجود دارد که می تواند به طور هم زمان در هر دو رابطه بالا صدق کند. بنابراین، مقدار θp1 از طریق این روابط قابل محاسبه است.

زاویه θp2، صفحه دربرگیرنده σ2 را نمایش می دهد. از آنجایی که صفحات دربرگیرنده تنش های اصلی بر هم عمود هستند، مقدار θp2 به اندازه 90 درجه کوچک تر یا بزرگ تر از زاویه θp1 خواهد بود.

مقدار تنش های برشی بر روی صفحات اصلی:
یکی از ویژگی های مهم صفحات اصلی، امکان تعیین آن ها با استفاده از معادلات تبدیل تنش های برشی است. اگر تنش برشی τx1y1 را برابر با صفر قرار دهیم، معادله زیر به دست می آید:

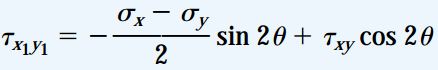
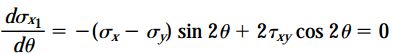
در صورت حل رابطه τx1y1 بر حسب tan2θ، به رابطه زیر می رسیم:

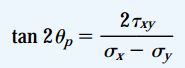
به عبارت دیگر، مقدار تنش های برشی بر روی صفحات اصلی صفر است.

حالت های خاص تنش های اصلی:
صفحات x و y در المان هایی که تحت تنش تک محوری و دومحوری قرار دارند، به عنوان صفحات اصلی آن ها در نظر گرفته می شوند (شکل زیر).

مقدار tan2θp در این حالت های خاص برابر با صفر و در نتیجه، زاویه θp دارای مقادیر 0 و 90 است. به علاوه، صفر بودن تنش های برشی بر روی صفحات x و y، یکی دیگر از دلایل اصلی بودن این صفحات به شمار می رود.

برای المان هایی که تحت برش خالص قرار دارند، صفحات اصلی نسبت به محور x به اندازه 45 درجه اختلاف زاویه دارند (شکل زیر). به دلیل بی نهایت بودن مقدار tan2θp در این وضعیت، زاویه θp دارای مقادیر 45 و 135 خواهد بود. اگر τxy مثبت باشد، مقدار تنش های اصلی σ1=τxy و σ2=-τxy است.

تنش اصلی سوم:
در بخش های قبلی، مبحث تنش های اصلی و دوران محورها را تنها در صفحه xy (دوران حول محور z) مورد بررسی قرار دادیم. تنش های اصلی محاسبه شده در این حالت با عنوان «تنش های اصلی درون صفحه ای» (In-Plane Principal Stresses) شناخته می شوند.

با همه این تفاسیر نباید سه بعدی بودن المان تنش در مسائل واقعی را نادیده بگیریم. در واقع، هر المان تنش دارای سه تنش اصلی اعمال شونده بر روی سه صفحه متعامد است.

با اجرای یک تحلیل سه بعدی کامل تر می توان مشاهده کرد که سه صفحه اصلی یک المان تنش از دو صفحه اصلی معرفی شده در بخش های قبلی و صفحه z المان تشکیل می شوند.

شکل زیر، سه صفحه اصلی یک المان تنش را نمایش می دهد. در شکل ب، المان تنش تحت زاویه اصلی θp1 دوران یافته است. مقادیر تنش های اصلی σ1 و σ2 با استفاده از رابطه کلی σ1,2 تعیین می شوند؛ در صورتی که تنش اصلی سوم (σ3) برابر با صفر در نظر گرفته شده است.

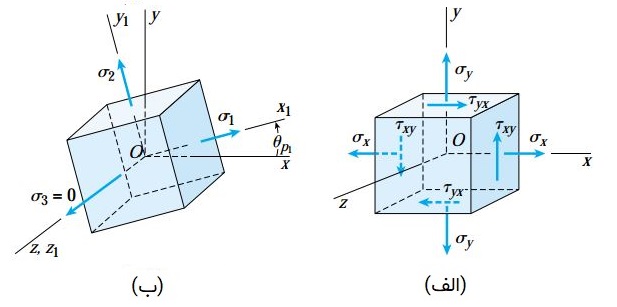
با توجه به تعاریف ارائه شده در بخش های قبلی، مقدار σ1 بزرگ تر از σ2 در نظر گرفته می شود. اگرچه، مقدار σ3 می تواند در محدوده ای کوچک تر، بزرگ تر یا بین σ1 و σ2 قرار داشته باشد.

علاوه بر این، امکان برابر بودن یک، دو یا هر سه تنش اصلی نیز وجود دارد. به خاطر داشته باشید که هیچ تنش برشی بر روی هیچ یک از صفحات اصلی رخ نمی دهد.