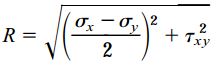مراحل رسم دایره مور

مراحل رسم دایره مور:
دایره مور را می توان با استفاده از روش های مختلفی رسم کرد. انتخاب هر یک از این روش ها به معلوم یا مجهول بودن مولفه های تنش بستگی دارد.

به منظور نمایش ویژگی های اصلی دایره مور، فرض می کنیم که مقادیر تنش های σy، σx و τxy بر روی صفحات x و y در یک المان تنش صفحه ای مشخص هستند (شکل زیر).

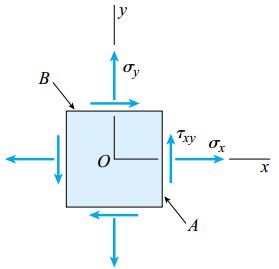
مشخص بودن این مقادیر برای رسم دایره مور کفایت می کند. با رسم دایره می توانیم مقادیر تنش های σy1، σx1 و τx1y1 بر روی یک المان دوران یافته مانند شکل زیر را محاسبه کنیم. علاوه بر این، تنش های اصلی و تنش های برشی ماکسیمم نیز قابل تعیین خواهند بود.

دایره مور نمایش داده شده در شکل زیر را در نظر بگیرید.

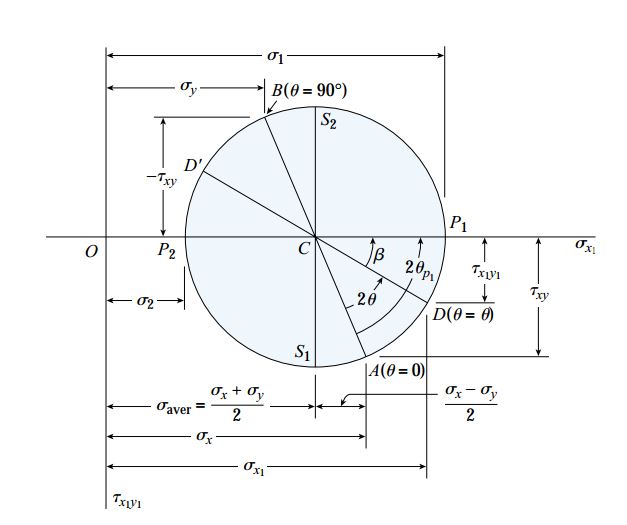
به منظور رسم این دایره باید مراحل زیر را انجام دهید:

• در ابتدا یک دستگاه محورهای مختصات با محور افقی σx1 (مقادیر مثبت در سمت راست) و محور عمودی τx1y1 (مقادیر مثبت در بخش پایین) را رسم کنید.
• محل قرارگیری مرکز دایره (نقطه C) را در مختصات σx1=σaver و τx1y1=0 مشخص کنید.
• محل قرارگیری نقطه A (معرف شرایط تنش بر روی صفحه x المان) را در مختصات σx1=σx و τx1y1=τxy مشخص کنید. توجه داشته باشید که زاویه مربوط به نقطه A بر روی دایره مور برابر با θ=0 در نظر گرفته می شود.
• محل قرارگیری نقطه B (معرف شرایط تنش بر روی صفحه y المان) را در مختصات σx1=σy و τx1y1=τxy مشخص کنید. توجه داشته باشید که زاویه مربوط به نقطه B بر روی دایره مور برابر با θ=90 در نظر گرفته می شود. نقاط معرف A و B بر روی المان تنش در شکل زیر نمایش داده شده اند.
• یک خط راست از نقطه A تا B رسم کنید. این خط همان قطر دایره است که از مرکز C عبور می کند. نقاط A و B، تنش های موجود بر روی صفحاتی با اختلاف 90 درجه را نمایش می دهند (شکل بالا). این نقاط بر روی دو انتهای قطر دایره قرار دارند. از این رو، اختلاف زاویه آن ها بر روی دایره 180 درجه است.
• با انتخاب نقطه C به عنوان مرکز، دایره مور را به گونه ای رسم می کنیم که از روی نقاط A و B عبور کند. شعاع دایره رسم شده با این روش R خواهد بود.

پس از رسم دایره و استفاده از روابط هندسی می توان نشان داد که خطوط CA و CB، شعاع های دایره هستند و طول آن ها برابر با R است. طول مختصات نقاط C و A به ترتیب با مقادیر σx+σy)/2) و σx برابری می کند.

از این رو، اختلاف بین طول این نقاط بر روی محور افقی برابر با σx-σy)/2) خواهد بود (شکل بالا).

به علاوه، نقطه A ارتفاعی برابر با τxy دارد. به این ترتیب، خط CA را می توان به عنوان وتر یک مثلث در نظر گرفت که طول یکی از اضلاع آن σx-σy)/2) و طول ضلع دیگر آن τxy است. با گرفتن جذر از مجموع مربعات این دو ضلع، رابطه شعاع دایره مور (R) به فرم زیر درمی آید:

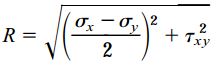
رابطه بالا مشابه رابطه معرفی شده در بخش معادلات دایره مور است. با یک روش مشابه می توانیم ثابت کنیم که طول خط CB با شعاع دایره (R) برابری می کند.