حالت های خاص قانون هوک برای تنش صفحه ای

حالت های خاص قانون هوک برای تنش صفحه ای:

در حالت «تنش دومحوری» (Biaxial Stress)، تنش برشی τxy برابر با صفر است. از این رو، قانون هوک برای تنش صفحه ای به شکل زیر درمی آید:

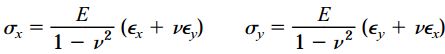
روابط بالا هیچ تفاوتی با روابط قبلی ندارند؛ چراکه تأثیر تنش های نرمال و برشی مستقل از یکدیگر است. در حالت «تنش تک محوری» (Uniaxial Stress)، تنش نرمال σy برابر با صفر خواهد بود. بنابراین، قانون هوک برای تنش صفحه ای ساده تر از حالت قبل می شود:

در حالت «برش خالص» (Pure Shear)، تنش های نرمال σy و σz برابر با صفر هستند. به این ترتیب، قانون هوک برای تنش صفحه ای به شکل زیر درمی آید:

در تمام این سه حالت خاص، مقدار تنش نرمال σz برابر با صفر است.

تغییرات حجم:
هنگامی که یک جسم جامد در معرض کرنش قرار می گیرد، علاوه بر ابعاد، حجم آن نیز تغییر می کند.

در صورت مشخص بودن مقادیر کرنش های نرمال در سه جهت عمود بر هم، میزان تغییر حجم جسم قابل محاسبه خواهد بود. برای نشان دادن نحوه انجام این محاسبات، المان کوچک نمایش داده شده در شکل زیر را در نظر بگیرید.

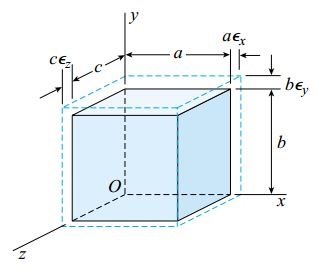
پیش از رخ دادن کرنش ها، طول ابعاد المان بالا در راستای y، x و z، به ترتیب برابر b، a و c است. با ایجاد کرنش های εy، εx و εz، ابعاد المان مطابق با خط چین نمایش داده شده در شکل بالا تغییر می کنند.

به این ترتیب، میزان افزایش طول هر بعد برابر با bεy، aεx و cεz خواهد بود. حجم اولیه المان (V0) از طریق رابطه زیر محاسبه می شود:

و حجم نهایی آن (V1) نیز به کمک رابطه زیر تعیین می شود:

با قرار دادن V0 به جای عبارت abc در رابطه، به رابطه زیر می رسیم:

اگر عبارت سمت راست رابطه بالا را بسط دهیم، رابطه زیر به دست می آید:

این روابط برای محاسبه کرنش های کوچک و کرنش های بزرگ قابل استفاده هستند. اگر میزان کرنش های به وجود آمده بسیار کوچک باشد، حاصل ضرب هر دو کرنش (مانند εxεy) در مقایسه با مقدار هر یک از کرنش ها (مانند εx یا εy) کوچک خواهد بود.

در این شرایط می توان از عبارت های شامل ضرب دو کرنش صرف نظر کرد. بنابراین، رابطه مربوط به محاسبه حجم نهایی المان به شکل زیر تغییر می کند:

به این ترتیب، اختلاف حجم المان برابر است با:

رابطه بالا برای اجسامی با کرنش های کوچک و یکنواخت کاربرد دارد. توجه داشته باشید که در این رابطه، پیروی ماده از قانون هوک ضروری نیست.

علاوه بر این، رابطه بالا نه تنها برای حالت تنش صفحه ای، بلکه برای تمام حالت های تنش قابل استفاده است.

به عنوان یک نکته تکمیلی باید اشاره کنیم که در اثر اعمال کرنش های برشی هیچ تغییری در حجم جسم رخ نمی دهد. تغییر حجم واحد (e) یا «اتساع» (Dilatation)، به صورت تغییرات حجم تقسیم بر حجم اولیه تعریف می شود.

بنابراین:

با به کارگیری این رابطه برای المان های حجم و انتگرال گیری از آن می توان تغییرات حجم یک جسم را حتی در صورت غیر یکنواخت بودن کرنش های نرمال محاسبه کرد.

معادلات ارائه شده هم برای کرنش های فشاری و هم برای کرنش های کششی قابل استفاده هستند. بر اساس قواعد علامت گذاری، افزایش حجم با علامت مثبت و کاهش حجم با علامت منفی نمایش داده می شود. این قاعده برای هر دو کمیت e و ΔV صادق است.

اکنون موادی را در نظر بگیرید که از قانون هوک پیروی می کنند و تنها در معرض تنش صفحه ای قرار دارند. در این شرایط، کرنش های εy، εx و εz با استفاده از معادلات ارائه شده در بخش های قبلی تعیین می شوند. با جایگذاری این معادلات در رابطه e خواهیم داشت:

توجه داشته باشید که رابطه بالا برای حالت تنش دومحوری نیز قابل استفاده است. در حالت تنش تک محوری، رابطه بالا به صورت زیر ساده می شود:

با توجه به این رابطه مشاهده می شود که بیشترین مقدار ممکن برای نسبت پواسون در مواد معمولی 0.5 است. اگر این مقدار بیشتر از 0.5 باشد، حجم در شرایط بارگذاری کششی کاهش می یابد. این مسئله خلاف رفتار فیزیکی مواد در حالت عادی است.

چگالی انرژی کرنشی در تنش صفحه ای:
چگالی انرژی کرنشی (u)، میزان انرژی کرنشی ذخیره شده در واحد حجم ماده را نمایش می دهد. به منظور آشنایی با نحوه تعیین این کمیت برای یک المان تحت تنش صفحه ای، شکل های زیر را در نظر بگیرید.

به دلیل مستقل بودن کرنش های نرمال و برشی از هم، انرژی کرنشی کل از جمع انرژی هر یک از این موارد به دست می آید.

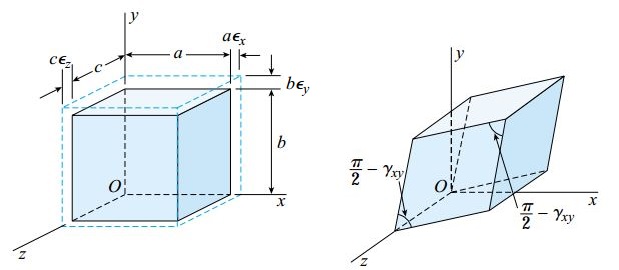
در مرحله اول، انرژی کرنشی ناشی از کرنش های نرمال را تعیین می کنیم. σx، تنش اعمال شده بر روی صفحه x را نمایش می دهد.

به این ترتیب، میزان نیروهای اعمال شده بر این صفحه از رابطه σxbc به دست می آید. با شروع بارگذاری، نیروهای اعمال شده از مقدار صفر به یک مقدار حداکثری می رسند. هم زمان با رخ دادن این فرآیند، صفحه x المان به اندازه aεx جابجا می شود.

کار انجام شده با حاصل ضرب نیرو در جابه جایی برابر است. بنابراین:

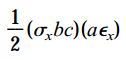
کاربرد این رابطه برای موادی است که از قانون هوک پیروی می کنند. به همین ترتیب، اعمال نیروی σyac بر روی صفحه y باعث انجام کاری معادل با عبارت زیر می شود:

با جمع دو عبارت قبلی، رابطه انرژی کرنشی ذخیره شده در المان مورد بررسی به دست می آید:

به این ترتیب، چگالی انرژی کرنشی ناشی از اعمال تنش ها و کرنش های نرمال برابر است با:

چگالی انرژی کرنشی ناشی از اعمال تنش ها و کرنش های برشی نیز عبارت است از:

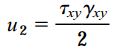
با جمع دو رابطه بالا، به رابطه چگالی انرژی کرنشی برای حالت تنش صفحه ای دست می یابیم:

با استفاده از معادلات قانون هوک می توان چگالی انرژی کرنشی را بر اساس مؤلفه های تنش بیان کرد:

به همین ترتیب، با استفاده از معادلات قانون هوک، رابطه چگالی انرژی کرنشی بر اساس مؤلفه های کرنش نیز قابل تعریف خواهد بود:

با حذف عبارات مربوط به برش (τxy یا γxy) در روابط بالا، معادله چگالی انرژی کرنشی برای حالت تنش دومحوری به دست می آید.

علاوه بر این، با در نظر گرفتن مقادیر زیر، معادله چگالی انرژی کرنشی برای حالت تنش تک محوری نیز تعیین می شود:

برای تعیین چگالی انرژی کرنش در حالت برش خالص، مقادیر زیر را در روابط اصلی جایگزین می کنیم: