تغییر طول غیر یکنواخت سازه های معین استاتیکی:
اعمال بارهای محوری نامعین بر روی میله ها:
شکل زیر را در نظر بگیرید. فرض کنید که نقاط میانی یک میله منشوری همانند این شکل در معرض یک یا چند بار محوری قرار گرفته اند.
در این شرایط، میزان تغییر طول کلی میله از جمع جبری تغییرات به وجود آمده در هر بخش آن به دست می آید. به منظور محاسبه این تغییر طول باید مراحل زیر را دنبال کنید:
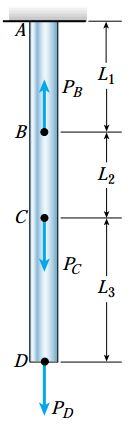
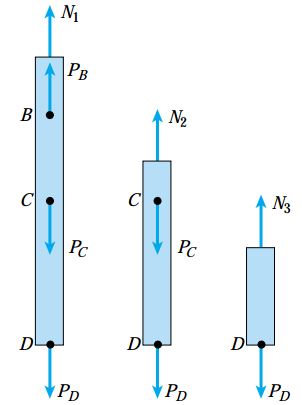
با جمع نیروهای عمودی در نمودارهای بالا، معادلات تعادل زیر به دست می آیند:
در این معادلات، علامت مثبت برای نیروهای داخلی کششی و علامت منفی برای نیروهای داخلی فشاری در نظر گرفته می شود.
گام سوم: تعیین تغییرات طول هر بخش با استفاده از روابط زیر:
L2، L1 و L3: طول بخش های 1، 2 و 3؛ EA: صلبیت محوری میله
گام چهارم: جمع تغییر طول های δ2، δ1 و δ3 به منظور تعیین تغییر طول ایجاد شده در کل میله (δ):
همان گونه که قبلاً نیز اشاره شد، مقادیر تغییر طول هر بخش به صورت جبری با هم جمع می شوند (علامت مثبت برای افزایش طول و علامت منفی برای کاهش طول).
میله های متشکل از چند بخش منشوری:
اگر میله ای از چندین بخش منشوری با ابعاد، مواد تشکیل دهنده یا نیروهای متفاوت تشکیل شده باشد، تعیین تغییر طول به وجود آمده در کل میله با استفاده از روش معرفی شده در بخش قبل صورت می گیرد.
رابطه تغییر طول کل برای این حالت به صورت زیر است:
i: اندیس نام گذاری بخش های مختلف میله؛ n: تعداد بخش ها؛ Ni: نیروی محوری داخلی در بخش i ام
تغییر پیوسته در ابعاد یا بارهای اعمال شده بر روی میله:
در برخی از مواقع، نیروی محوری N و مساحت سطح مقطع A به طور پیوسته در راستای محور میله تغییر می کنند.
نمونه ای از این وضعیت در شکل زیر نمایش داده شده است. در این میله، نه تنها مساحت سطح مقطع بلکه نیروی محوری نیز در راستای محور طولی میله به طور پیوسته تغییر می کند. با توجه به شکل، بارگذاری دارای دو بخش متفاوت است.
تک نیروی PB بر انتهای میله (در نقطه B) و بارهای توزیع شده (p(x در راستای محور میله اعمال می شوند.
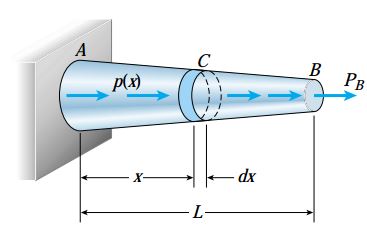
توجه: نیروی توزیع شده بر حسب نیرو بر واحد فاصله (مانند نیوتن بر متر یا پوند بر اینچ) بیان می شود. این نوع نیرو توسط عواملی نظیر نیروهای گریز از مرکز، نیروهای اصطکاکی یا وزن میله آویزان در یک موقعیت عمودی به وجود می آیند.
در این شرایط نمی توانیم رابطه معرفی شده برای حالت قبلی (تغییر طول میله چندبخشی) را مورد استفاده قرار دهیم. در عوض باید ابتدا تغییر طول یک المان کوچک از میله را تعیین کنیم و سپس از طول میله انتگرال بگیریم. به این منظور، المان dx در فاصله x از انتهای چپ میله را در نظر می گیریم.
نیروی محوری داخلی (N(x در این مقطع (شکل وسط) با کمک معادلات تعادل بخش AC یا CB و رسم نمودار جسم آزاد تعیین می شود. به طور کلی، این نیرو تابعی از x است.
با مشخص بودن ابعاد میله می توان مساحت سطح مقطع (A(x را نیز به صورت تابعی از x نمایش داد.
تغییر طول المان dx با dδ نمایش داده می شود. با قرار دادن (N(x به جای P، dx به جای L و (A(x به جای A در رابطه δ=PL/EA، رابطه زیر برای تعیین dδ به دست می آید:
با انتگرال گیری از رابطه بالا، تغییر طول کل میله محاسبه می شود:
اگر عبارت های (N(x و (A(x پیچیده نباشند، انتگرال بالا به صورت تحلیلی قابل حل خواهد بود. در این صورت، یک فرمول برای محاسبه δ به دست می آید (مانند مثال 2 در انتهای مقاله). اگرچه، در صورت دشوار یا غیرممکن بودن انتگرال بالا باید از یک روش عددی به منظور حل مسئله استفاده کرد.
محدودیت های موجود در روابط ارائه شده:
روابط ارائه شده در بخش های قبلی تنها برای مواد الاستیک خطی قابل استفاده هستند (وجود پارامتر E در تمام روابط). به علاوه، فرمول δ=PL/EA با فرض یکنواخت بودن تنش بر روی سطح مقطع میله به دست آمده است.
این فرض در میله های منشوری صدق می کند و در میله هایی با سطح مقطع متغیر اعتباری ندارد. به همین دلیل، تنها در صورت کوچک بودن زاویه بین دو طرف این میله ها، نتایج به دست آمده از رابطه زیر قابل قبول خواهند بود:
با توجه به بررسی های صورت گرفته، اگر زاویه بین دو طرف میله برابر با 20 درجه باشد، تنش به دست آمده از رابطه σ=P/A (در یک مقطع دلخواه)، 3 درصد کمتر از مقدار دقیق تنش به دست آمده از روش های پیشرفته خواهد بود. برای زوایای کوچک، خطای محاسبات کمتر می شود.
بنابراین، هر چه زاویه تغییر سطح مقطع میله کمتر باشد، نتایج به دست آمده از رابطه بالا قابل قبول تر خواهد بود.
در صورت بزرگ بودن زاویه تغییر سطح مقطع میله، باید از روش های دقیق تر استفاده کرد.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
