تأثیر تغییر دما روی تغییر طول سازه ها

تأثیر تغییر دما روی تغییر طول سازه ها:
تغییر دمای سازه باعث انبساط یا انقباض مواد تشکیل دهنده و ایجاد «تنش حرارتی» (Thermal Stress) و «کرنش حرارتی» (Thermal Strain) در آن می شود.

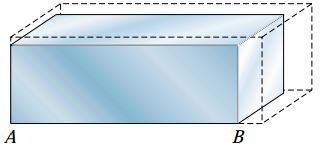
شکل زیر، نمونه ساده ای از انبساط حرارتی یک بلوک را نمایش می دهد. صفحات این بلوک تحت هیچ محدودیتی قرار ندارند و می توانند آزادانه حرکت پیدا کنند.

با افزایش دمای بلوک، المان های تشکیل دهنده آن در راستای تمام جهات با کرنش های حرارتی مواجه می شوند.

به این ترتیب، ابعاد بلوک افزایش می یابد. اگر گوشه A را به عنوان یک نقطه مرجع (ثابت) در نظر بگیریم و بگذاریم ضلع AB راستای اصلی خود را حفظ کند، شکل بلوک مطابق خط چین های نمایش داده شده در شکل زیر تغییر خواهد کرد.

در اکثر مواد، میزان کرنش حرارتی εT با تغییرات دما ΔT متناسب است:

کمیت α، یکی از خواص ماده موسوم به «ضریب انبساط حرارتی» (Coefficient of Thermal Expansion) است.

به دلیل بی بعد بودن کمیت کرنش، واحد ضریب انبساط حرارتی برابر با معکوس واحد دما در نظر گرفته می شود. در سیستم SI می توان α را با یکی از واحدهای معکوس کلوین یا معکوس درجه سلسیوس بیان کرد.

به دلیل برابر بودن اختلاف دما در هر دو واحد کلوین و درجه سلسیوس، مقدار α در هر دو حالت یکسان خواهد بود. در سیستم واحدهای آمریکایی، α بر حسب معکوس فارنهایت بیان می شود.

به عنوان یک قاعده کلی در نظر داشته باشید که در هنگام محاسبه کرنش های حرارتی، معمولاً علامت مثبت برای انبساط و علامت منفی برای انقباض مورد استفاده قرار می گیرد.

برای نمایش اهمیت کرنش های حرارتی، آن ها را با کرنش های ناشی از اعمال بار مقایسه می کنیم.

یک میله تحت بار محوری با کرنش طولی ε=σ/E را در نظر بگیرید (σ، تنش و E، مدول الاستیسیته میله را نمایش می دهد).

سپس، فرض کنید که یک میله مشابه دیگر در معرض تغییر دمای ΔT و کرنش حرارتی ε=αΔT قرار گرفته است. با برابر قرار دادن این دو کرنش، معادله زیر حاصل می شود:

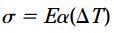
σ، تنش محوری مورد نیاز برای ایجاد کرنشی برابر با کرنش حاصل از تغییر دمای ΔT را نمایش می دهد.

به عنوان مثال، یک میله فولادی ضد زنگ با مدول الاستیسیته E=30×106psi و ضریب انبساط گرمایی α=9.6×10-6/F را در نظر بگیرید.

با قرار دادن این مقادیر در معادله بالا می توان مشاهده کرد که اگر دمای میله را به اندازه 100 درجه فارنهایت تغییر دهیم، میزان کرنش حرارتی با کرنش ناشی از اعمال تنش 29000 پوند بر اینچ مربعی برابر خواهد بود.

این میزان تنش در محدوده تنش های مجاز برای فولاد ضد زنگ قرار دارد.

به این ترتیب، تغییرات نسبتاً کوچک دما می توانند به اندازه بارهای معمولی باعث ایجاد کرنش درون سازه شوند. این مسئله، اهمیت تأثیر دما بر روی طراحی های مهندسی را نمایش می دهد.

مواد ساختمانی در هنگام افزایش دما، منبسط و هنگام کاهش دما، منقبض می شوند. به این ترتیب، علامت کرنش حرارتی در حین افزایش دما مثبت است.

کرنش های حرارتی معمولاً برگشت پذیر هستند. بنابراین در صورت بازگشت دما به مقدار اولیه، شکل عضوهای سازه نیز به حالت اولیه خود بازمی گردد.

با این وجود، تعداد کمی از آلیاژهای فلزی جدید از این رفتار پیروی نمی کنند.

در این مواد خاص، افزایش دما باعث کاهش ابعاد و کاهش دما باعث افزایش ابعاد سازه می شود. رفتار آب از نقطه نظر حرارتی به عنوان یکی از موارد خاص به شمار می رود.

نکته غیر معمول در مورد آب این است که پس از رسیدن به دمای 4 درجه سلسیوس، افزایش و کاهش دما باعث افزایش حجم ماده می شوند. در نتیجه، حداکثر چگالی آب در دمای 4 درجه سلسیوس رخ می دهد.

اکنون بلوک زیر را در نظر بگیرید. فرض می کنیم که ماده تشکیل دهنده این بلوک، همگن و همسانگرد است. به علاوه، افزایش دمای ΔT نیز به صورت یکنواخت درون بلوک ایجاد می شود.

با در نظر گرفتن این فرضیات می توانیم میزان افزایش ابعاد بلوک را با ضرب طول اولیه در کرنش حرارتی محاسبه کنیم.

به عنوان مثال، اگر یکی از ابعاد بلوک برابر L باشد، میزان افزایش این بعد با استفاده از رابطه زیر به دست می آید:

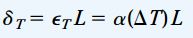
این رابطه، یک رابطه دما-جابه جایی و معادلِ رابطه نیرو-جابه جایی در مبحث «تحلیل سازه های نامعین استاتیکی» است.

به منظور محاسبه تغییر طول عضوهایی که تحت تغییرات یکنواخت دما قرار گرفته اند می توان از رابطه دما-جابه جایی استفاده کرد.

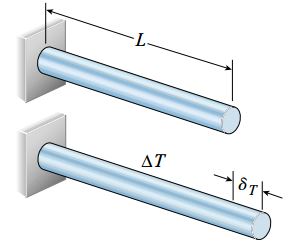
شکل زیر، نمونه ای از افزایش طول δT ناشی تغییرات یکنواخت دما در یک میله منشوری را نمایش می دهد. (توجه داشته باشید که بعد جانبی میله نیز در اثر افزایش دما تغییر می کند اما به دلیل عدم تأثیر این تغییرات بر روی انتقال بارهای محوری توسط میله، از نمایش آن ها بر روی شکل صرف نظر شده است.)

در بخش های قبلی فرض کردیم که هیچ عامل محدودکننده ای برای انبساط یا انقباض سازه وجود ندارد.

این شرایط برای اجسام ساکن بر روی یک سطح بدون اصطکاک یا اجسام آویزان در فضای باز صدق می کند. در این موارد، بر اثر تغییرات یکنواخت دما هیچ تنشی درون شی رخ نمی دهد.

با این وجود، تغییرات غیر یکنواخت دما می توانند باعث ایجاد تنش های داخلی شوند. تکیه گاه های موجود در اکثر سازه ها از انبساط یا انقباض آزادانه جلوگیری می کنند.

در این موارد، تغییرات یکنواخت دما نیز منجر به گسترش تنش های حرارتی درون سازه می شوند.

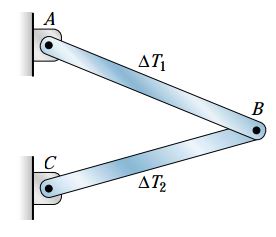
برای آشنایی با پیامدهای اثرات حرارتی، خرپای نمایش داده شده در شکل زیر را در نظر بگیرید. سپس، فرض کنید که دمای میله AB به اندازه ΔT1 و دمای میله BC به اندازه ΔT2 تغییر می کند.

این سازه از نظر استاتیکی معین است. بنابراین، امکان افزایش یا کاهش طول آزادانه هر دو میله و در نتیجه جابه جایی مفصل B وجود دارد.

در این حالت، هیچ تنشی در میله ها و هیچ عکس العملی در تکیه گاه ها رخ نمی دهد.

در سازه های معین استاتیکی، تغییرات یکنواخت دما باعث ایجاد کرنش های حرارتی و تغییر طول عضوهای سازه می شوند اما هیچ تنشی در این فرآیند به وجود نمی آید.

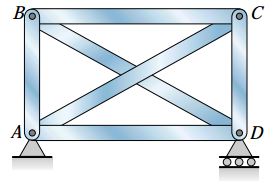
در سازه های نامعین استاتیکی شرایط متفاوت است. در این سازه ها، ایجاد تنش های حرارتی به مواد تشکیل دهنده و ماهیت تغییرات دما بستگی دارد. برای آشنایی با سناریوهای مختلف، سازه نمایش داده شده در شکل زیر را در نظر بگیرید.

به دلیل فراهم بودن امکان حرکت افقی در مفصل D، هیچ تنشی در هنگام افزایش یکنواخت دمای خرپا به وجود نمی آید. در این شرایط، طول تمام عضوهای سازه متناسب با طول اولیه خود افزایش می یابد و اندازه خرپا کمی بزرگ تر می شود.

اگر افزایش دما تنها بر روی برخی از میله ها اعمال شود، آرایش نامعین استاتیکی میله ها از انبساط آزادانه سازه جلوگیری می کند و باعث ایجاد تنش های حرارتی درون سازه می شود.

برای تصور این وضعیت، فرض کنید که تنها دمای یکی از میله ها افزایش یافته است.

با افزایش طول این میله، میله های دیگر در برابر تغییرات آن مقاومت می کنند و باعث ایجاد تنش در تمام عضوهای سازه می شوند.

تحلیل یک سازه نامعین استاتیکی در هنگام وجود تغییرات دما بر اساس مفاهیم معادلات تعادل، معادلات سازگاری و روابط جابه جایی صورت می گیرد.

تفاوت اصلی در این تحلیل ها، استفاده از روابط دما-جابه جایی به همراه روابط نیرو-جابه جایی (δ=PL/AE) برای حل مسئله است.