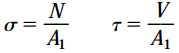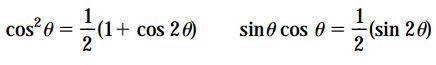مولفه های تنش روی صفحات مورب(مقطع عرضی)

مولفه های تنش روی صفحات مورب(مقطع عرضی):

شکل زیر، یک میله منشوری تحت بارهای محوری P را نمایش می دهد. با در نظر گرفتن مقطعی در میانه میله (مانند مقطع mn) می توانیم نمودار جسم آزاد بخشی از میله را رسم کنیم.

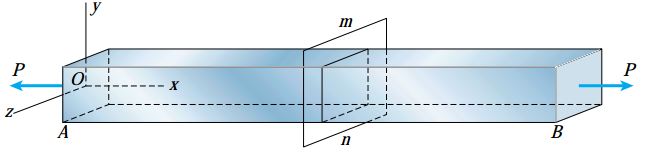
در صورت منشوری بودن میله (یکنواخت بودن سطح مقطع در راستای محور طولی)، همگن بودن مواد تشکیل دهنده آن، اعمال بار محوری P بر روی مرکز هندسی سطح مقطع و فاصله کافی مقطع مورد نظر از نواحی تمرکز تنش، توزیع تنش درون میله یکنواخت خواهد بود.

به این ترتیب می توان مقدار تنش های نرمال اعمال شده بر روی مقطع mn را با استفاده از رابطه σx=P/A محاسبه کرد. در شکل زیر، مقطع mn بر محور طولی میله عمود است و به همین دلیل، هیچ تنش برشی بر روی این مقطع وجود ندارد.

برای راحتی بیشتر محاسبات، معمولاً به جای به کارگیری نمای پیچیده سه بعدی (شکل بالا) از نمای دوبعدی (شکل زیر) به منظور نمایش وضعیت تنش بر روی مقاطع میله استفاده می شود.

اگرچه، در هنگام استفاده از نمای دوبعدی باید ضخامت میله در راستای عمود بر صفحه را نیز برای انجام محاسبات در نظر داشته باشید.

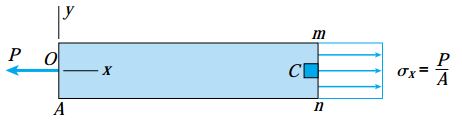
حالت تنش بر روی یک مقطع عرضی:
کاربردی ترین روش برای نمایش تنش های میله نمایش شده در بخش قبلی، جدا کردن یک المان کوچک از ماده (مانند المان C در شکل زیر) و رسم تنش های اعمال شده بر روی تمام صفحات آن است.

به این نوع المان، «المان تنش» (Stress Element) گفته می شود. المان تنش در نقطه C، یک بلوک کوچک مربعی یا مستطیلی است که صفحه سمت راست آن بر روی مقطع mn قرار دارد.

در تئوری، ابعاد یک المانِ تنش بی نهایت کوچک است اما به منظور نمایش واضح تر مؤلفه های تنش، این المان با مقیاس بزرگ رسم می شود (مانند شکل زیر). اضلاع المان نمایش داده شده در شکل زیر با محورهای y، x و z موازی هستند و تنها تنش های نرمال σx بر روی صفحه x اعمال می شوند.

حالت تنش بر روی صفحات مورب:
المان تنش نمایش داده شده در بخش قبلی، تنها نمای محدودی از تنش های درون یک میله در شرایط بارگذاری محوری را نمایش می دهد.

برای درک بهتر و کامل تر حالت تنش، باید مولفه های اعمال شده بر روی صفحات مورب را مورد ارزیابی قرار دهیم. به عنوان مثال، مقطع به وجود آمده از صفحه مورب pq در میله زیر را در نظر بگیرید.

با فرض یکسان بودن میزان تنش در تمام نقاط میله، توزیع تنش های اعمال شده بر روی مقطع مورب به صورت یکنواخت خواهد بود.

نحوه توزیع تنش ها بر روی این مقطع، در نمودار جسم آزاد سه بعدی و دوبعدی زیر نمایش داده شده است. با در نظر گرفتن شرایط تعادلِ جسمِ آزاد، برآیند تنش ها باید برابر با نیروی افقی P باشد (خط چین نمایش داده شده در دو شکل زیر).

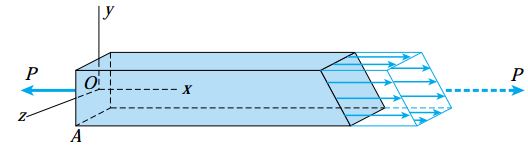
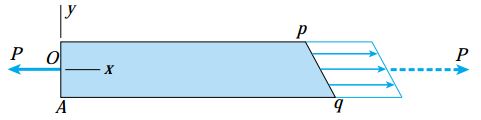
به عنوان یک نکته ابتدایی در نظر داشته باشید که برای مشخص کردن جهت گیری مقطع مورب pq باید از یک قاعده کلی استفاده کنیم.

معمولاً زاویه θ بین محور x و بردار نرمال n به عنوان جهت گیری مقطع مورب در نظر گرفته می شود. برای مقطع pq در شکل های بالا، زاویه θ حدود 30 درجه است. برای مقطع mn، به دلیل هم جهت بودن بردار نرمال و محور x، مقدار زاویه θ صفر بود.

برای درک بهتر این موضوع، المان مکعبی بخش قبل را در نظر بگیرید. در این المان، زاویه θ برای صفحه سمت راست 0 درجه، برای صفحه بالایی 90 درجه، برای صفحه سمت چپ 180 درجه و برای صفحه پایینی 270 یا 90- درجه است.

با در نظر گرفتن توضیحات بالا، تنش های اعمال شده بر روی مقطع مورب pq را تعیین می کنیم. همان طور که قبلاً از نیز اشاره شد، برآیند این تنش ها با نیروی P در راستای x برابر است.

این نیروی برآیند را می توان به دو مؤلفه تجزیه کرد. مؤلفه اول، نیروی نرمال N در راستای عمود بر سطح مقطع pq و مؤلفه دوم، نیروی برشی V در راستای مماس بر این مقطع خواهد بود.

به منظور تعیین مؤلفه های حاصل از تجزیه نیروی برآیند P از روابط زیر استفاده می کنیم:

تنش های نرمال و برشی نیز به ترتیب بر اثر اعمال نیروهای N و V بر روی مقطع مورب ایجاد می شوند. توجه داشته باشید که توزیع این تنش ها بر روی pq به صورت یکنواخت است.

مقدار تنش نرمال از تقسیم نیروی نرمال N بر مساحت سطح مقطع و مقدار تنش برشی نیز از تقسیم نیروی برشی V بر مساحت سطح مقطع محاسبه می شود. بنابراین:

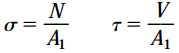
A1، مساحت سطح مقطع مورب را نمایش می دهد و با استفاده از رابطه زیر به دست می آید:

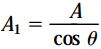
به طور معمول، مساحت سطح مقطع عمود بر محور طولی میله با A نمایش داده می شود. با توجه به شکل های بالا، جهت اعمال تنش نرمال σ و تنش برشی τ به ترتیب با جهت اعمال نیروی نرمال N و نیروی برشی V یکسان است.

به منظور جلوگیری از اشتباهات در محاسبات باید یک قاعده استاندارد برای نام گذاری و علامت گذاری تنش های اعمال شده بر روی مقاطع مورب را مورد استفاده قرار دهیم.

به این ترتیب، برای نمایش تنش های اعمال شده بر روی یک مقطع مورب تحت زاویه θ از اندیس θ و برای نمایش تنش های اعمال شده بر روی یک مقطع عمود بر محور x از اندیس x استفاده می کنیم.

علاوه بر این، تنش های نرمال σθ در شرایط بارگذاری کششی را با علامت مثبت و تنش های برشی τθ در شرایط دوران پادساعت گرد ماده را با علامت منفی نمایش می دهیم.

به عنوان مثال، تنش های نرمال و برشی نمایش داده شده در شکل زیر مثبت هستند.

برای یک میله تحت کشش، نیروی نرمال N باعث ایجاد تنش های نرمال مثبت و نیروی برشی V باعث ایجاد تنش های برشی منفی می شود. مقادیر این تنش ها با استفاده از معادلات زیر به دست می آیند:

رابطه کلی σx=P/A برای تعیین تنش نرمال بر روی یک مقطع و همچنین با روابط مثلثاتی زیر را در نظر بگیرید:

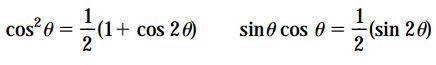
با استفاده از روابط بالا، به معادلات زیر برای تعیین تنش های نرمال و برشی دست می یابیم:

این معادلات، مقادیر تنش های اعمال شده بر روی یک مقطع مورب تحت زاویه θ نسبت به محوری x را تعیین می کنند.

به عنوان یک نکته مهم در نظر داشته باشید که معادلات بالا تنها با استفاده از روابط استاتیکی به دست آمده اند و هیچ ارتباطی با خواص ماده ندارند.

از این رو، این معادلات برای تمام مواد (خطی یا غیر خطی، الاستیک یا غیر الاستیک) قابل استفاده هستند.