کرنش های برشی بر روی سطح خارجی میله

کرنش های برشی بر روی سطح خارجی میله:
میله زیر و المانی از آن را در نظر بگیرید. این المان بین دو سطح مقطع با فاصله dx از یکدیگر قرار دارد. بر روی سطح خارجی المان، المان کوچک abcd را مشخص می کنیم.

اضلاع ab و cd با محور طولی میله موازی هستند. در حین اعمال پیچش، سطح مقطع سمت راست به اندازه زاویه کوچک dφ نسبت به سطح مقطع سمت چپ دوران می کند.

به این ترتیب، نقاط b و c به سمت نقاط ‘b و ‘c جابجا می شوند. در حین دوران المان، تغییری در طول اضلاع المان کوچک رخ نمی دهد.

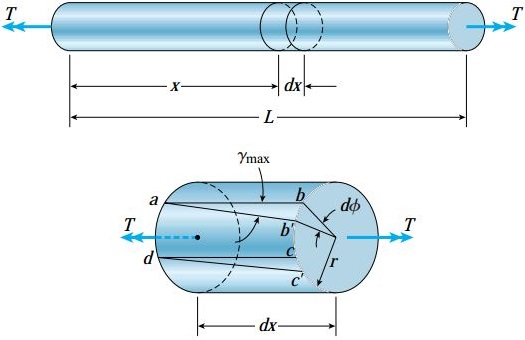
پس از اعمال پیچش، زوایای گوشه های المان ab’c’d تغییر می کنند و دیگر برابر با 90 درجه نخواهند بود.

با توجه به ایجاد کرنش برشی و عدم وجود کرنش های نرمال، این المان تحت برش خالص قرار خواهد داشت.

مقدار کرنش برشی در سطح خارجی میله (γmax) با میزان کاهش زاویه در نقطه a (کاهش زاویه گوشه bad) برابر است.

با توجه به شکل بالا، میزان کاهش این زاویه از رابطه زیر به دست می آید:

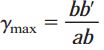
γmax: کرنش برشی بر حسب رادیان؛ b’b: میزان جابه جایی نقطه b؛ و ab: طول المان (dx)

با در نظر گرفتن r به عنوان شعاع میله، میزان جابه جایی نقطه b (فاصله b’b) با استفاده از رابطه rdφ قابل محاسبه خواهد بود (dφ برحسب رادیان بیان می شود).

بنابراین:

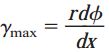
این معادله برای محاسبه کرنش برشی بر روی سطح خارجی میله، با توجه به زاویه پیچش مورد استفاده قرار می گیرد.

کمیت dφ/dx، نرخ تغییرات زاویه پیچش φ نسبت به فاصله x بر روی محور میله است. این کمیت با علامت θ نمایش داده شده و با عنوان «نرخ پیچش» (Rate of Twist) یا زاویه پیچش بر واحد طول شناخته می شود:

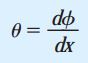
با استفاده از این مفهوم می توانیم معادله کرنش برشی در سطح خارجی میله را به صورت زیر بازنویسی کنیم:

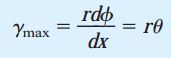
برای به دست آوردن معادلات θ و γmax، میله را تحت پیچش خالص در نظر گرفتیم. با این وجود، هر دو معادله مذکور برای شرایط کلی تر پیچش نیز قابل استفاده هستند.

به عنوان مثال، اگر نرخ پیچش θ ثابت نباشد و مقدار آن نسبت به فاصله x در امتداد محور میله تغییر کند نیز می توانیم معادلات بالا را مورد استفاده قرار دهیم.

در حالت خاص پیچش خالص، نرخ پیچش با تقسیم زاویه پیچش کل (φ) بر طول میله (L) برابر است:

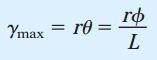
این معادله را می توان از طریق روابط هندسی شکل زیر نیز به دست آورد. γmax، زاویه بین خطوط pq و ’pq (زاویه گوشه ’qpq) را نمایش می دهد.

بنابراین، γmaxL با فاصله q’q در انتهای میله برابر خواهد بود. به دلیل برابر بودن ’qq با rφ، به رابطه rφ=γmaxL می رسیم. این رابطه با معادله بالا مطابقت دارد.