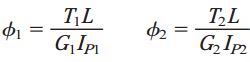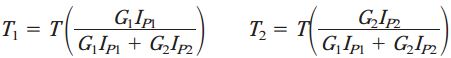مراحل تحلیل پیچش سازه های استاتیکی نامعین:
به منظور تحلیل مؤلفه های پیچش در سازه های نامعین استاتیکی، چهار گام کلی وجود دارد:
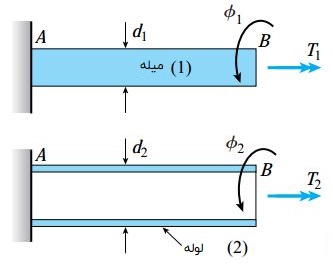
به منظور آشنایی با نحوه به کارگیری مراحل بالا در تحلیل پیچش سازه های نامعین استاتیکی، میله کامپوزیتی نمایش داده شده در شکل زیر را در نظر بگیرید.
انتهای A به یک تکیه گاه ثابت متصل شده و انتهای B در معرض گشتاور پیچشی T قرار گرفته است.
این سازه از یک میله توپر و یک لوله تشکیل می شود. میله و لوله به یک صفحه صلب در انتهای B متصل شده اند.
به منظور سادگی بیشتر تحلیل، ویژگی های میله توپر و لوله را به با اعداد 1 و 2 مشخص می کنیم. به عنوان مثال، قطر میله توپر با d1 و قطر خارجی لوله با d2 مشخص می شود.
به دلیل وجود یک فضای خالی کوچک بین لوله و میله، قطر داخلی لوله کمی بزرگ تر از d1 است. با اعمال گشتاور پیچشی T بر روی میله کامپوزیتی، صفحه انتهایی تحت زاویه کوچک φ دوران می کند.
به علاوه، گشتاورهای پیچشی T1 و T2 نیز به ترتیب در میله توپر و لوله گسترش می یابند (شکل زیر).
جمع گشتاورهای ایجاد شده در میله توپر و لوله باید با میزان گشتاور اعمال شده به مجموعه میله کامپوزیتی برابر باشد. از این رو، معادله تعادل برای این مجموعه به صورت زیر نوشته می شود:
به دلیل کافی نبودن معادلات مورد نیاز برای تعیین مجهولات مسئله (یک معادله و دو مجهول)، میله کامپوزیتی از نظر استاتیکی نامعین خواهد بود.
از این رو، به منظور تعیین مجهولات مسئله به یک معادله دیگر نیاز خواهیم داشت.
برای دستیابی به معادله دوم، جابه جایی های دورانی میله توپر و لوله را در نظر می گیریم. زاویه پیچش میله توپر را با φ1 و زاویه پیچش لوله را با φ2 مشخص می کنیم.
به دلیل اتصال میله توپر و لوله به یک صفحه مشترک، این دو بخش تحت یک زاویه پیچش یکسان دوران می کنند. با توجه به این نکته، معادله سازگاری این مسئله به صورت زیر خواهد بود:
زوایای φ1 و φ2 از طریق روابط گشتاور-جابه جایی با کمیت های T1و T2 ارتباط پیدا می کنند.
در مواد الاستیک خطی، φ=TL/GIP به عنوان رابطه گشتاور-جابه جایی در نظر گرفته می شود. به این ترتیب:
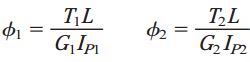
G1 و G2: مدول برشی مواد؛ IP1 و IP2؛ ممان اینرسی قطبی مقاطع عرضی
با جایگذاری روابط بالا در φ1=φ2 می توان معادله سازگاری را بر حسب مجهولات T1 و T2 بازنویسی کرد:
اکنون با حل هم زمان معادله بالا و معادله تعادل، روابط مورد نیاز برای تعیین T1 و T2 به دست می آیند:
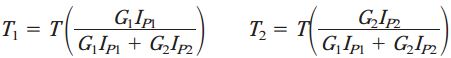
با معلوم شدن گشتاورهای مورد نیاز، بخش اصلی تحلیل سازه نامعین استاتیکی به پایان می رسد. در این مرحله، کمیت هایی نظیر تنش و زاویه پیچش نیز قابل تعیین خواهند بود.
در این مقاله، روش کلی تحلیل یک سازه نامعین استاتیکی در شرایط بارگذاری پیچشی را مورد بررسی قرار دادیم.
در بخش بعدی، نحوه استفاده از این روش برای تحلیل یک میله الاستیک خطی را توضیح خواهیم داد.
توجه داشته باشید که این فرآیند کلی را می توان برای مواد غیر خطی نیز به کار برد.
تنها تفاوت بین تحلیل مواد خطی و غیر خطی در روابط گشتاور-جابه جایی مرتبط با هر یک از آن ها است.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
