خانه
اپلیکیشن زینگ
آشنایی و همکاری
سامانه صادرات و واردات
فروشگاه
خدمات اطلاعاتی
اخبار و مقالات
تماس با ما


انرژی کرنشی و ثابت پیچش در لوله:

با استفاده از تعیین انرژی کرنشی یک المان و انتگرال گیری در محدوده آن می توان انرژی کرنشی یک لوله جدار نازک را محاسبه کرد.
المانی با مساحت سطح مقطع tds و طول dx را در نظر بگیرید. حجم این المان برابر با tdsdx است.
به دلیل قرار داشتن لوله در معرض برش خالص، چگالی انرژی کرنشی المان برابر با τ2/2G خواهد بود. به این ترتیب، انرژی کرنشی کل از ضرب چگالی انرژی کرنشی در حجم به دست می آید:
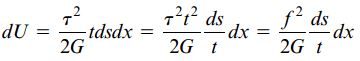
به جای عبارت τt در رابطه بالا از کمیت جریان برش f به عنوان یک پارامتر ثابت استفاده شده است. برای تعیین انرژی کرنشی کل لوله باید از du انتگرال گیری کنیم. به این منظور، از ds در محدوده 0 تا Lm (طول خط میانی) و از dx در محدوده 0 تا L (طول لوله) انتگرال می گیریم. به این ترتیب:
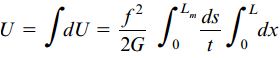
توجه داشته باشید که ضخامت t می تواند در اطراف خط میانی تغییر می کند. از این رو، کمیت مذکور باید به همراه ds در انتگرال قرار داشته باشد. حاصل انتگرال آخر در رابطه بالا با طول لوله برابر است. به همین دلیل، رابطه انرژی کرنشی به صورت زیر درمی آید:
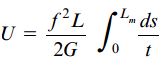
با جایگذاری رابطه جریان برش در این رابطه، خواهیم داشت:
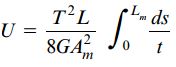
این جایگذاری به منظور بازنویسی رابطه انرژی کرنشی بر حسب گشتاور پیچشی T صورت می گیرد. عبارت بالا را می توان به فرم ساده تری تبدیل کرد.
این کار با معرفی یک ویژگی جدید به نام «ثابت پیچش» (Torsion Constant) صورت می گیرد. ثابت پیچش، یکی از ویژگی های سطح مقطع جسم به شمار می رود.
برای یک لوله جدار نازک، این ثابت به صورت زیر تعریف می شود:
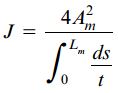
با در نظر گرفتن مفهوم ثابت پیچش، معادله انرژی کرنشی به فرم زیر درمی آید:
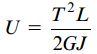
این رابطه با رابطه معرفی شده برای تعیین انرژی کرنشی یک لوله دایره ای شکل شباهت دارد. تنها تفاوت بین این دو رابطه، قرارگیری ثابت پیچش J به جای ممان اینرسی قطبی Ip است.
توجه داشته باشید که ثابت پیچش بر حسب واحد طول به توان چهار بیان می شود. اگر ضخامت سطح مقطع لوله ثابت باشد، رابطه J ساده تر خواهد شد:
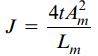
با استفاده روابط معرفی شده برای J می توانیم ثابت پیچش سطح مقطعی با هر شکل دلخواه را محاسبه کنیم. لوله جدار نازک دایره ای زیر را در نظر بگیرید. به دلیل ثابت بودن ضخامت، از رابطه بالا برای تعیین ثابت پیچش استفاده می کنیم.
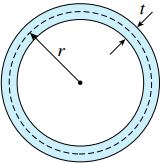
با جایگذاری Lm=2πr و Am=πr2 به رابط زیر می رسیم:
![]()
این رابطه، با رابطه تقریبی ممان اینرسی قطبی برابر است. بنابراین، در لوله های جدار نازک دایره ای، ممان اینرسی قطبی با ثابت پیچش برابر خواهد بود. اکنون یک لوله مستطیلی مطابق شکل زیر را در نظر بگیرید.
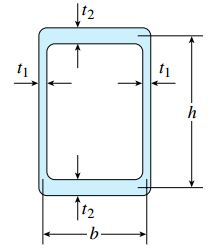
برای این لوله، Am=bh است. بنابراین، انتگرال موجود در رابطه ثابت پیچش آن به صورت زیر حل می شود:
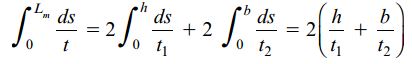
به این ترتیب، رابطه ثابت پیچش لوله جدار نازک مستطیلی با ضخامت ثابت برابر است با:
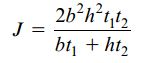
ثابت پیچش لوله های جدار نازک با سطح مقطع های دیگر نیز به همین ترتیب تعیین می شوند.