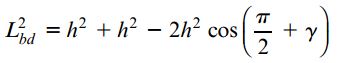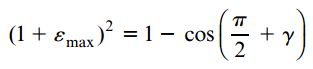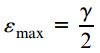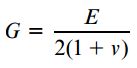تعیین رابطه بین مدول الاستیسیته و مدول برشی با مفاهیم پیچش

تعیین رابطه بین مدول الاستیسیته و مدول برشی با مفاهیم پیچش:

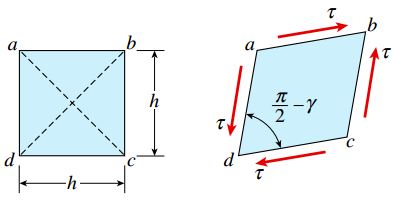
شکل زیر، المان تنش abcd را نمایش می دهد. صفحه جلویی abcd به شکل یک مربع در نظر گرفته می شود. طول اضلاع این مربع، h است.

در صورت اعمال تنش های برشی τ و ایجاد برش خالص در این المان، صفحه جلویی آن به شکل یک لوزی درمی آید.

پس از این فرآیند، طول اضلاع المان تغییریافته برابر با h و تنش برشی ایجاد شده در آن γ=τ/G خواهد بود. به دلیل ایجاد اعوجاج، طول قطر bd افزایش و طول قطر ac کاهش می یابد.

طول قطر bd با حاصل ضرب طول اولیه آن در ضریب 1+εmax برابر است:

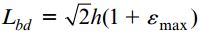
Lbd: طول قطر bd المان؛ h: طول اضلاع المان تنش؛ 0.5(2)*h: طول اولیه قطر bd المان؛ εmax: تنش نرمال در راستای 45 درجه

با در نظر گرفتن هندسه المان تغییریافته می توان رابطه بین کرنش برشی γ و طول قطر bd را تعیین کرد. به این منظور، المان مثلثی abd را مطابق شکل زیر در نظر می گیریم.

این المان، نصفِ المان تغییریافته را نمایش می دهد. طول ضلع bd برابر با Lbd و طول دیگر اضلاع برابر با h است. زاویه adb نیز با نصف زاویه adc یا π/4-γ/2 برابری می کند. مقدار زاویه abd نیز مشابه زاویه adb خواهد بود.

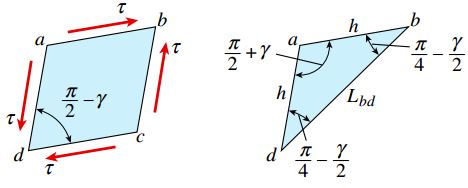
با توجه به موارد بالا، زاویه dab با π/2+γ برابر بوده و رابطه زیر بین اضلاع المان مثلثی برقرار است:

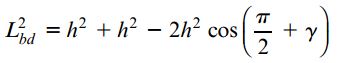
با جایگذاری رابطه Lbd در معادله بالا و ساده سازی طرفین معادله، خواهیم داشت:

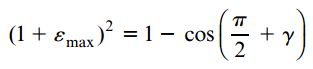
اگر عبارت سمت چپ معادله بالا را باز کنیم و با توجه به قواعد مثلثاتی، (cos(π/2+γ را برابر با sinγ- قرار دهیم:

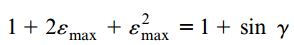
از آنجایی که کرنش های εmax و γ بسیار کوچک هستند، می توان از عبارت ε2)max) صرف نظر کرد و γ را به جای sinγ قرار داد. به این ترتیب، معادله بالا به رابطه زیر تبدیل خواهد شد:

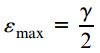
این رابطه، یکی از روابط به دست آمده در مبحث «تعیین مؤلفه های تنش و کرنش در بارگذاری پیچشی» است.

بر اساس روابط به دست آمده در این مبحث می توانیم از τ(1+ν)/E به جای εmax و بر اساس قانون هوک در مواد تحت برش می توانیم از τ/G به جای کرنش برشی γ در رابطه بالا استفاده کنیم. با اعمال این جایگذاری ها خواهیم داشت:

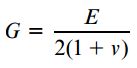
این فرآیند به ما نشان می دهد که کمیت های G، E و ν (نسبت پواسون) به عنوان خواص مستقل مواد الاستیک خطی به شمار نمی روند.

به این ترتیب، با مشخص بودن دو مورد از این کمیت ها می توان کمیت سوم را نیز محاسبه کرد.