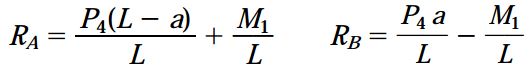عکس العمل های تکیه گاهی در تیرها:

خمشی4

تیر ساده:
شکل زیر، تیر ساده ای با یک تکیه گاه لولایی و یک تکیه گاه غلتکی را نمایش می دهد. سازه AB تحت نیروی مورب P1، نیروی عمودی P2 و بار یکنواختی با شدت q قرار گرفته است.

با توجه به پیکربندی تیر AB می توان دریافت که سه عکس العمل تکیه گاهی مجهول در این مسئله وجود دارد (نیروی افقی HA در تکیه گاه لولایی، نیروی عمودی RA در تکیه گاه لولایی و نیروی عمودی RB در تکیه گاه غلتکی).

برای سازه های ساده ای مانند تیر AB، هر سه معادله تعادل با استفاده از قواعد استاتیکی به دست می آیند.

به دلیل برابر بودن تعداد معادلات و مجهولات مسئله (سه مجهول و سه معادله تعادل)، سازه مورد بررسی از نظر استاتیکی معین خواهد بود. معادله تعادل نیروهای موجود در تیر AB در راستای افقی به صورت زیر نوشته می شود:

به این ترتیب داریم:

این معادله به اندازه ای واضح و مشخص است که معمولاً با استفاده از مشاهده پیکربندی تیر به دست می آید. به منظور تعیین عکس العمل های عمودی RA و RB، به ترتیب معادلات تعادل گشتاور حول نقاط B و A را می نویسیم.

اگر علامت گشتاور ساعت گرد را مثبت در نظر بگیریم، خواهیم داشت:

خمشی2

با حل معادلات بالا بر حسب RA و RB به معادلات زیر می رسیم:

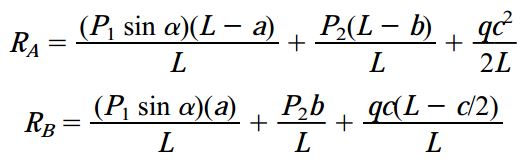
تیر یکسر گیردار:
برای حالت بعدی، تیر یکسر گیردار زیر را در نظر بگیرید. همان گونه که مشاهده می کنید؛ یک نیروی مورب P3 و یک بار متغیر بر روی این سازه اعمال می شود. بار متغیر اعمال شده بر روی تیر، به وسیله یک نمودار شدت بار ذوزنقه ای نمایش داده شده است که محدوده آن از q1 تا q2 تغییر می کند.

بر اساس پیکربندی تیر، یک نیروی عکس العمل افقی (HA)، یک نیروی عکس العمل عمودی (RA) و یک کوپل (MA) در سازه وجود خواهد داشت. با توجه به تعادل نیروها در راستای افقی، یکی از معادلات تعادل به دست می آید:

تعادل نیروها در راستای عمودی نیز تعیین رابطه بعدی را امکان پذیر می کند:

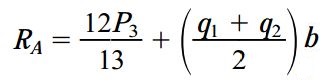
توجه داشته باشید که برآیند نیروی گسترده با مساحت نمودار بارگذاری (ذوزنقه) برابر است. در معادله بالا از این نکته برای محاسبه نیروی عکس العمل RA استفاده کردیم (عبارت سمت راست).

گشتاور عکس العمل MA در تکیه گاه گیردار با استفاده از معادله تعادل گشتاورها به دست می آید. در این مثال، به منظور حذف HA و RA از معادله مورد نظر، گشتاورهای حول نقطه A را با هم جمع خواهیم کرد. به علاوه، برای تعیین گشتاور بار گسترده نیز ذوزنقه تشکیل شده را به دو مثلث مجزا تقسیم می کنیم (خط چین شکل زیر).

برآیند هر یک از این مثلث ها، نیرویی هم اندازه با مساحت مثلث مورد نظر خواهد بود. علاوه بر این، خط اثر هر نیروی برآیند از مرکز هندسی مثلث مربوطه عبور خواهد کرد.

به این ترتیب، گشتاورهای بار گسترده حول نقطه A از رابط زیر به دست می آید:

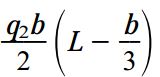
q1b/2: نیروی برآیند مثلث بار پایینی (مساحت مثلث پایینی)؛ L-2b/3: بازوی گشتاور نیروی برآیند مثلث پایینی؛ q2b/2: نیروی برآیند مثلث بار بالایی (مساحت مثلث بالایی)؛ L-b/3: بازوی گشتاور نیروی برآیند مثلث بالایی

با توجه به روابط مربوط به گشتاورهای بار گسترده، معادله تعادل گشتاور به صورت زیر خواهد بود (گشتاور پادساعت گرد مثبت در نظر گرفته شده است):

خمشی3

بنابراین:

به دلیل مثبت بودن نتیجه معادله بالا، جهت اعمال گشتاور عکس العمل MA با جهت فرضی ما (پادساعت گرد) هم راستا خواهد بود.

تیر ساده با انتهای آزاد:
شکل زیر، یک تیر ساده با انتهای آزاد را نمایش می دهد. این تیر در معرض یک نیروی عمودی (P4) و یک کوپل گشتاور (M1) قرار گرفته است.

به دلیل عدم اعمال نیروهای افقی بر روی تیر، عکس العمل موجود در تکیه گاه لولایی فاقد مؤلفه های افقی بوده و رسم این مؤلفه ها در نمودار جسم آزاد ضروری نخواهد بود.

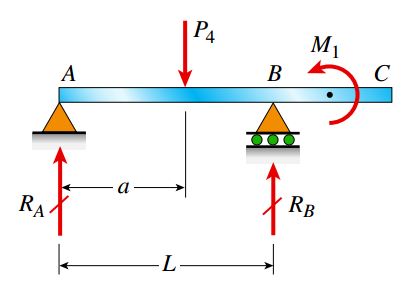
اکنون می توانیم با استفاده از معادله تعادل گشتاورهای حول نقطه A و B، عکس العمل های تکیه گاهی را محاسبه کنیم (علامت گشتاورها را در جهت پادساعت گرد مثبت در نظر می گیریم):