رابطه بین بار، نیروی برشی و گشتاور خمشی (بار متمرکز)

رابطه بین بار، نیروی برشی و گشتاور خمشی (بار متمرکز):

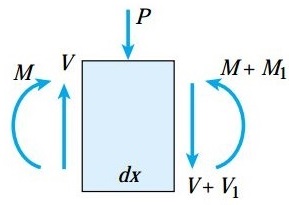
در این بخش، یک بار متمرکز اعمال شده بر روی المان تیر را مورد بررسی قرار می دهیم. با در نظر گرفتن تعادل نیروها در راستای عمودی، خواهیم داشت:

این رابطه نشان می دهد که در محل اعمال یک بار متمرکز، مقدار نیروی برشی با یک تغییر ناگهانی مواجهه خواهد شد. با عبور از محل اعمال این بار، میزان نیروی برشی به اندازه P کاهش می یابد. اگر گشتاورهای حول صفحه سمت چپ المان را با هم جمع کنیم، به معادله زیر می رسیم:

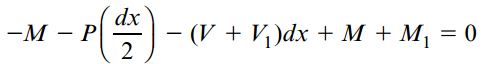
فرم ساده تر این معادله به صورت زیر نوشته می شود:

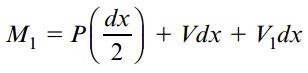
از آنجایی که طول المان مورد بررسی بسیار کوچک است (dx)، میزان افزایش گشتاور خمشی نیز کوچک خواهد بود (M1). به همین دلیل، مقدار گشتاور خمشی با عبور از روی نقطه اعمال بار متمرکز تقریباً تغییر نمی کند.

با وجود عدم تغییر گشتاور خمشی M در محل اعمال بار متمرکز، نرخ آن (dM/dx) در معرض یک تغییر ناگهانی قرار می گیرد.

در ضلع سمت چپ المان، نرخ تغییرات گشتاور خمشی برابر با dM/dx=V است. این نرخ در سمت راست المان به مقدار dM/dx=V+V1=V-P می رسد.

در نتیجه، نرخ تغییرات گشتاور خمشی در محل اعمال بار متمرکز به اندازه آن بار (P) کاهش می یابد.

کوپل:
در بخش آخر این مقاله، تأثیر اعمال کوپل بر روی روابط بین نیروهای برشی و گشتاورهای خمشی را مورد بررسی قرار می دهیم.

با در نظر گرفتن تعادل نیروهای اعمال شده در راستای عمودی، V1=0 خواهد بود. این مسئله نشان می دهد که مقدار نیروی برشی در محل اعمال کوپل تغییری نمی کند.

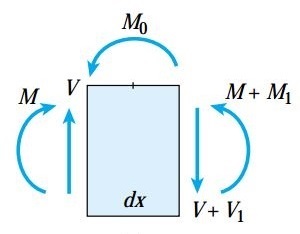
در صورت جمع کردن گشتاورهای حول صفحه سمت چپ المان به رابطه زیر می رسیم:

با صرف نظر کردن از عبارات دارای مقادیر دیفرانسیلی (به دلیل کوچک بودن مقدار آن ها)، خواهیم داشت:

بر اساس این رابطه، با حرکت بر روی طول المان، مقدار گشتاور خمشی در محل اعمال کوپل به اندازه M0 کاهش می یابد. بنابراین، گشتاور خمشی در این نقطه با یک تغییر ناگهانی مواجه خواهد شد.