نمودار نیروی برشی و گشتاور خمشی (بار متمرکز)

نمودار نیروی برشی و گشتاور خمشی (بار متمرکز):

تیر ساده زیر را در نظر بگیرید. بار متمرکز P بر روی تیر AB اعمال می شود. فاصله این بار تا تکیه گاه سمت چپ تیر برابر با a و فاصله آن تا تکیه گاه سمت راست برابر با b است.

اگر نمودار جسم آزاد کل تیر را در نظر بگیریم، عکس العمل های تکیه گاهی آن با استفاده از معادلات تعادل به دست می آیند:

در مرحله بعد، تیر AB را در فاصله x از تکیه گاه A برش می دهیم. سپس، نمودار جسم آزاد بخش سمت چپ تیر را مطابق شکل زیر رسم می کنیم.

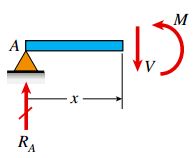
با توجه به معادلات تعادل این جسم آزاد، روابط مورد نیاز برای تعیین نیروی برشی V و گشتاور خمشی M در فاصله x از تکیه گاه A به صورت زیر خواهند بود:

این روابط، تنها برای بخش سمت چپ بار P اعتبار دارند. در مرحله بعد، سمت راست بار P (فاصله ای بین a تا L) بر روی تیر را برش می دهیم. سپس، نمودار جسم آزاد بخش سمت چپ تیر را مطابق شکل زیر رسم می کنیم.

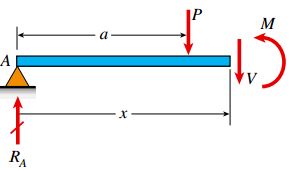
با توجه به معادلات تعادل این جسم آزاد، روابط مورد نیاز برای تعیین نیروی برشی و گشتاور خمشی به دست می آیند:

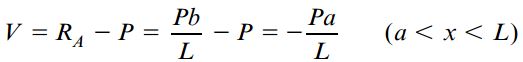
و

توجه داشته باشید که این روابط فقط برای بخش سمت چپ تیر اعتبار دارند. شکل زیر، نمودار نیروی برشی و نمودار گشتاور خمشی تیر AB را نمایش می دهد. این نمودارها با استفاده از روابط به دست آمده برای بخش سمت راست و چپ بار متمرکز P رسم شده اند.

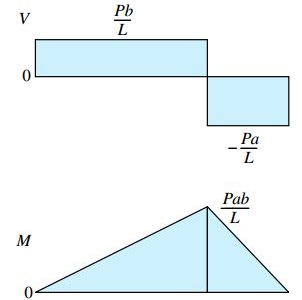
با توجه به نمودار نیروی برشی می توان مشاهده کرد که مقدار نیروی برشی در تکیه گاه A (فاصله x=0) با مقدار عکس العمل RA برابر است.

این نیرو تا رسیدن به نقطه اعمال بار P ثابت باقی می ماند. سپس، مقدار آن در نقطه اعمال بار به صورت ناگهانی و به اندازه P کاهش می یابد.

در بخش سمت راست تیر نیز مانند بخش سمت چپ، میزان نیروی برشی ثابت است اما مقدار عددی آن با عکس العمل موجود در نقطه B برابری می کند.

بر اساس نمودار گشتاور خمشی، این گشتاور در سمت چپ تیر از مقدار صفر در تکیه گاه A تا مقدار Pab/L در محل اعمال بار متمرکز (فاصله x=a) به صورت خطی افزایش می یابد.

در بخش سمت راست نیز گشتاور خمشی از مقدار Pab/L در محل اعمال بار تا مقدار صفر در تکیه گاه B (فاصله x=L) به صورت خطی کاهش می یابد. به این ترتیب، گشتاور خمشی ماکسیمم برابر است با:

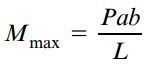
این گشتاور در محل اعمال بار متمرکز رخ می دهد. روابط مربوط به تعیین نیروی برشی و گشتاور خمشی موجود در سمت راست محل اعمال بار با توجه به معادلات تعادل جسم آزاد بخش سمت چپ تیر به دست می آیند (شکل زیر).

این جسم آزاد در معرض نیروهای RA و P به علاوه V و M قرار دارد. در این مثال به خصوص، استفاده از بخش سمت راست تیر به عنوان جسم آزاد، تحلیل مسئله را ساده تر می کند؛ چراکه در این حالت تنها یک نیرو (RB) به علاوه V و M در معادلات تعادل وجود خواهند داشت.

توجه داشته باشید که استفاده از هر کدام از این نمودارها (سمت چپ یا راست تیر)، تغییری در نتایج به دست آمده ایجاد نمی کند.

اکنون می توانیم برخی از ویژگی های نمودارهای نیروی برشی و گشتاور خمشی تیر AB را مورد تحلیل قرار دهیم.

با توجه به نمودار نیروی برشی، شیب dV/dx در بازه های 0 تا a و a تا L برابر با صفر است. این نتیجه با معادله dV/dx=-q مطابقت دارد.

بر اساس نمودار گشتاور خمشی، شیب dM/dx در بازه های 0 تا a و a تا L با مقدار نیروی برشی V برابری می کند.

در بخش سمت چپ بار P، شیب نمودار گشتاور خمشی مثبت و برابر با Pb/L است. بخش سمت راست بار، یک شیب منفی با مقدار Pa/L- دارد.

به این ترتیب، در محل اعمال بار، نمودار نیروی برشی با یک تغییر ناگهانی (به اندازه P) و نمودار گشتاور خمشی با یک تغییر شیب مواجه می شود.

در این مرحله از تحلیل، مساحت زیر نمودار نیروی برشی را مورد بررسی قرار می دهیم. در محدوده x=0 تا x=a، مساحت نمودار نیروی برشی برابر با Pab/L است. این کمیت، افزایش گشتاور خمشی به اندازه Pab/L در محدوده مذکور را نمایش می دهد.

در فاصله x=a تا x=L، مساحت نمودار نیروی برشی با مقدار Pab/L- برابری می کند. منفی بودن این مساحت، بیانگر کاهش گشتاور خمشی به اندازه Pab/L- در محدوده مورد بررسی است. در نهایت، گشتاور خمشی در تکیه گاه B به مقدار صفر می رسد.

اگر گشتاورهای خمشی موجود در هر دو تکیه گاه تیر برابر با صفر باشند، مساحت نمودار نیروی برشی در محدوده x=0 تا x=L صفر خواهد بود.

معمولاً این حالت را می توان در تیرهای ساده ای مشاهده کرد که هیچ کوپلی بر روی آن ها اعمال نمی شود.

به خاطر داشته باشید که در طراحی تیرها از مقادیر ماکسیمم و مینیمم نیروهای برشی استفاده می شود.

برای یک تیر ساده با یک بار متمرکز، نیروی برشی ماکسیمم در تکیه گاه نزدیک به محل اعمال بار و گشتاور خمشی ماکسیمم در زیر محل اعمال بار رخ می دهد.