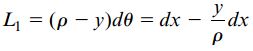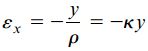تعیین کرنش درون تیرها (کرنش طولی)

تعیین کرنش درون تیرها (کرنش طولی):
کرنش های طولی موجود در یک تیر را می توان با تحلیل انحنای تیر و تغییر شکل های مربوط به آن اندازه گیری کرد.

برای آشنایی با نحوه تعیین این کرنش ها، بخشی از یک تیر تحت خمش خالص را در نظر بگیرید. شکل زیر، بخش AB تیری را نمایش می دهد که در معرض گشتاورهای خمشی مثبت M قرار دارد.

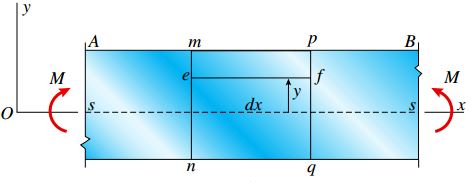
به منظور تحلیل تیر AB، فرض می کنیم که محور طولی آن پیش از اعمال گشتاور به صورت مستقیم بوده و مقطع عرضی آن نسبت به محور y دارای تقارن است (شکل زیر).

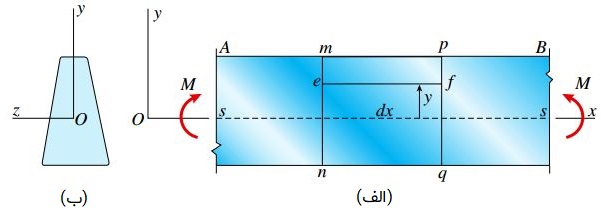
با اعمال گشتاور خمشی، تیر در صفحه xy (صفحه خمش) تغییر شکل می دهد و محور طولی آن به شکل یک منحنی دایره ای درمی آید (منحنی s-s در شکل زیر). به دلیل خمیدگی رو به بالای تیر، انحنای آن مثبت در نظر گرفته می شود.

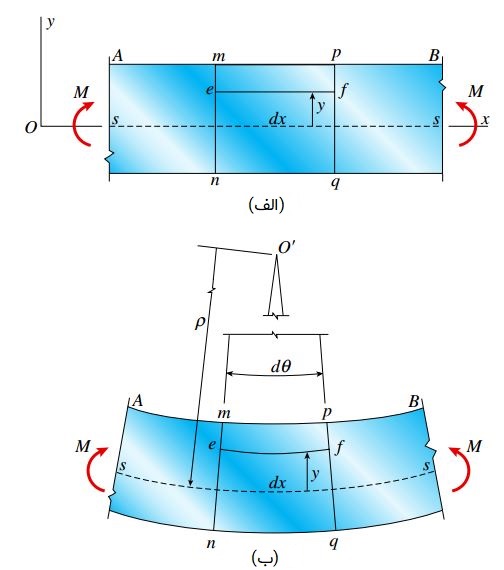
پس از اعمال گشتاور خمشی و ایجاد تغییر شکل، سطح مقطع هایی نظیر مقطع mn و pq به صورت صفحه ای و عمود بر محور طولی تیر باقی می مانند.

این موضوع یکی از نکات اساسی در حوزه تحلیل تیر به شمار می رود و در اغلب موارد از آن به عنوان یک فرضیه یاد می شود.

با این وجود، در صورت به کارگیری دلایل منطقی مبتنی بر تقارن هندسی تیرها می توان نکته مذکور را به عنوان یک تئوری علمی نیز در نظر گرفت.

به این ترتیب، در صورت وجود تقارن در شکل تیر و نحوه بارگذاری، تمام المان های تیر (نظیر المان mpqn) باید به صورت یکسان تغییر شکل دهند.

این نتیجه گیری به ماده تشکیل دهنده تیرها (الاستیک یا غیر الاستیک، خطی یا غیر خطی) بستگی ندارد و برای تمام مواد صادق است.

با این وجود، خواص رفتاری مواد در جهت های مختلف باید نسبت به صفحه خمش دارای تقارن باشد.

توجه: با وجود صفحه ای ماندن مقاطع عرضی تیر در شرایط خمش خالص، امکان رخ دادن تغییر شکل در صفحه قرارگیری مقطع وجود دارد. این تغییر شکل ها به دلیل وجود اثرات نسبت پواسون ایجاد می شوند.

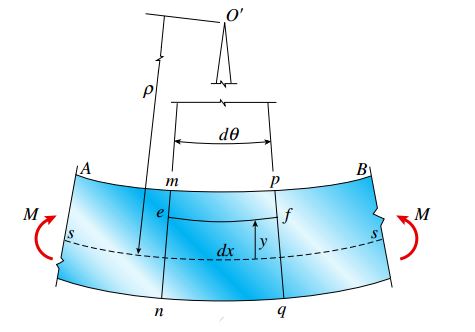
به دلیل خمیدگی های نمایش داده شده در شکل بالا، مقاطع mn و pq حول محورهای عمود بر صفحه xy نسبت به یکدیگر دوران می کنند.

خطوط طولی موجود بر روی بخش پایینی تیر با افزایش طول و خطوط طولی موجود بر روی بخش بالایی با کاهش طول مواجه می شوند.

به این ترتیب، بخش پایینی در معرض کشش و بخش بالایی در معرض فشار قرار می گیرد. در محلی میان بخش بالایی و پایینی، سطحی وجود دارد که طول خطوط موجود بر روی آن ثابت باقی می ماند.

به این سطح، «صفحه خنثی» (Neutral Surface) می گویند (خط چین s-s در شکل زیر). به تقاطع این صفحه با مقاطع عرضی تیر، «محور خنثی» (Neutral Axis) گفته می شود.

به عنوان مثال، محور z برای مقطع عرضی نمایش داده شده در شکل زیر، یک محور خنثی به شمار می رود.

پس از ایجاد تغییر شکل تیر، صفحه دربرگیرنده مقاطع عرضی mn و pq در مرکز انحنای ‘O با هم تقاطع پیدا می کنند (شکل بالا).

زاویه بین این صفحات با dθ و فاصله ‘O تا صفحه خنثی s-s با ρ (شعاع انحنا) نمایش داده می شود. طول اولیه خط dx بین دو مقطع مذکور بر روی سطح خنثی ثابت باقی می ماند.

در نتیجه، رابطه ρdθ=dx بین کمیت های این مسئله برقرار است. با این وجود، تمام خطوط طولی موجود بر روی صفحات دیگر با افزایش یا کاهش طول مواجه می شوند. این تغییرات «کرنش نرمال» (Normal Strain) را درون تیر به وجود می آورند (εx).

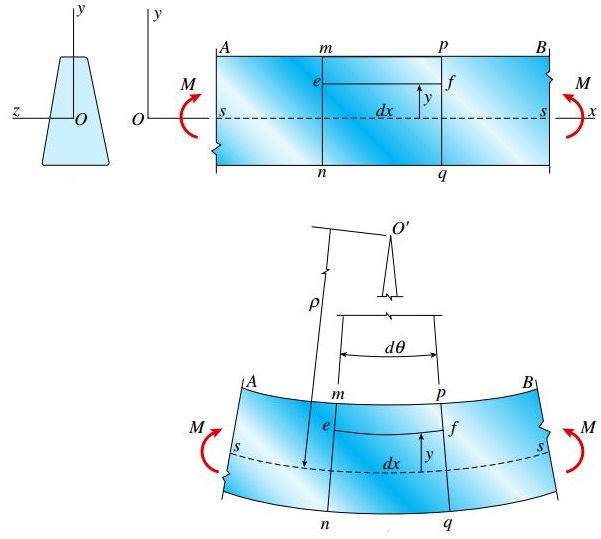
به منظور ارزیابی کرنش های به وجود آمده، خط طولی ef را در میان تیر و بین دو صفحه mn و pq در نظر می گیریم.

سپس، موقعیت قرارگیری این خط با فاصله آن تا سطح خنثی در تیر اولیه را مشخص می کنیم. این فاصله با حرف y نمایش داده می شود.

اکنون فرض می کنیم که محور x بر روی سطح خنثی اولیه قرار دارد. با تغییر شکل تیر، موقعیت این سطح تغییر می کند اما محور x ثابت باقی می ماند.

با این اوصاف پس از تغییر شکل تیر، فاصله بین خط طولی ef و صفحه خنثی تغییر نخواهد کرد و برابر با همان فاصله y خواهد بود.

طول خط ef پس از تغییر شکل تیر از رابطه زیر به دست می آید:

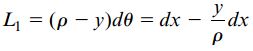
L1: طول خط ef پس از تغییر شکل تیر

از آنجایی که طول اولیه ef برابر با dx است، میزان افزایش طول از رابطه L1-dx یا ydx/ρ- به دست می آید. کرنش طولی مربوط به این تغییرات با تقسیم افزایش طول بر طول اولیه تعیین می شود. به این ترتیب، «رابطه کرنش-انحنا» (Strain-Curvature Relation) با معادله زیر برابر خواهد بود:

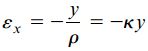
معادله بالا نشان می دهد که کرنش های طولی درون یک تیر با انحنای آن رابطه مستقیم دارند و نسبت به فاصله y از صفحه خنثی به طور خطی تغییر می کنند.

اگر نقطه مورد بررسی در بالای صفحه خنثی قرار گرفته باشد، مقدار y مثبت خواهد بود. به این ترتیب، در صورت مثبت بودن انحنا، کرنش منفی می شود.

کرنش منفی، کاهش طول را نمایش می دهد. در طرف مقابل، اگر نقطه مورد بررسی در پایین صفحه خنثی قرار گرفته باشد، مقدار y منفی خواهد بود.

بنابراین، در صورت مثبت بودن انحنا، کرنش مثبت می شود. کرنش مثبت، افزایش طول را نمایش می دهد.

توجه داشته باشید که قاعده علامت گذاری εx با قاعده علامت گذاری کرنش های نرمال شباهت دارد (علامت مثبت برای افزایش طول و علامت منفی برای کاهش طول).