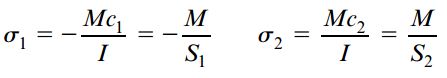تنش های نرمال موجود در تیرها (رابطه خمش)

تنش های نرمال موجود در تیرها (رابطه خمش):
با تعیین محل قرارگیری محور خنثی و رابطه گشتاور-انحنا، امکان محاسبه تنش های موجود در تیر بر اساس گشتاور خمشی فراهم می شود.

اگر رابطه انحنا را در σx=-Eκy جایگذاری کنیم، به معادله زیر خواهیم رسید:

این معادله با عنوان «رابطه خمش» (Flexure Formula) شناخته می شود و رابطه مستقیم بین تنش با گشتاور خمشی و رابطه عکس بین تنش با ممان اینرسی سطح مقطع را نمایش می دهد.

علاوه بر این، تنش های موجود در تیر با تغییر فاصله y (فاصله از محور خنثی) به صورت خطی تغییر می کنند.

تنش های به دست آمده از رابطه خمش با عنوان «تنش خمشی» (Bending Stress یا Flexural Stress) شناخته می شوند.

در صورت مثبت بودن گشتاور خمشی تیر، تنش های خمشی بر روی بخشی از سطح مقطع با فاصله منفی از محور خنثی دارای علامت مثبت (کششی) خواهند بود.

این تنش ها در بخش بالایی تیر با علامت منفی (فشاری) ظاهر می شوند. اگر علامت گشتاور خمشی منفی شود، علامت تنش ها برعکس خواهد شد (شکل زیر).

تنش های ماکسیمم موجود روی سطح مقطع:
تنش های کششی و فشاری ماکسیمم موجود بر روی هر سطح مقطع دلخواه، در نقاطی با بیشترین فاصله از محور خنثی رخ می دهند.

در شکل بالا، c1 و c2 به ترتیب فاصله محور خنثی از دورترین المان های موجود در جهت منفی و مثبت هستند.

به این ترتیب، تنش های نرمال ماکسیمم بر روی این نقاط به صورت زیر خواهند بود:

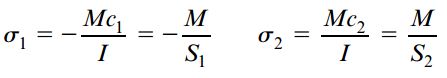
که در آن ها:

کمیت های S1 و S2 با عنوان «مدول مقطع» (Section Modulus) شناخته می شوند.

با توجه به روابط بالا، مدول مقطع دارای واحد طول به توان سه (in3 یا mm3) است.

علاوه بر این، توجه داشته باشید که فواصل c1 و c2 نسبت به بالا و پایین تیر همیشه مثبت در نظر گرفته می شوند.