تنش های نرمال موجود در تیرها (رابطه بین گشتاور و انحنا)

رابطه بین گشتاور و انحنا:
دومین معادله استاتیک بیان می کند که برآیند گشتاور تنش های نرمال σx با گشتاور خمشی M برابر است.

در صورت مثبت بودن σx، المان نیروی σxydA بر روی المان سطح dA دارای جهت گیری مثبت و در صورت منفی بودن σx، این المان دارای جهت گیری منفی خواهد بود.

به دلیل قرارگیری dA در بالای محور خنثی، تنش مثبت σx بر روی المان سطح اعمال می شود و یک المان گشتاور با مقدار σxydA را به وجود می آورد.

این المان گشتاور در خلاف جهت گشتاور خمشی مثبت M عمل می کند.

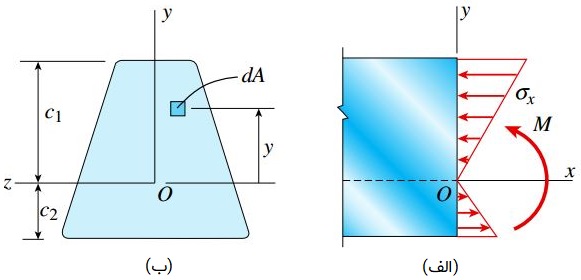
با توجه به شکل بالا و مطالب ارائه شده، خواهیم داشت:

به این ترتیب، انتگرال تمام المان های موجود بر روی سطح مقطع A باید با گشتاور خمشی M برابر باشد:

با جایگذاری σx=-Eκy در انتگرال بالا، به معادله زیر می رسیم:

این معادله، رابطه بین انحنای تیر و گشتاور خمشی را نمایش می دهد. از آنجایی که انتگرال موجود در معادله بالا به عنوان یکی از خواص سطح مقطع تیر در نظر گرفته می شود، بازنویسی این معادله به صورت زیر مناسب تر خواهد بود:

در این معادله:

این انتگرال با عنوان ممان اینرسی سطح مقطع نسبت محور z (محور خنثی) شناخته می شود. مقدار ممان اینرسی همیشه مثبت و واحد آن با طول به توان چهار برابر است.

به عنوان مثال، به منظور تحلیل تیرها در سیستم SI، این کمیت با واحد mm4 و در سیستم یکاهای آمریکایی با واحد in4 مورد محاسبه قرار می گیرد.

در صورت بازنویسی معادله M=κEI می توانیم میزان انحنای تیر را بر حسب گشتاور خمشی تعیین کنیم:

رابطه بالا، «معادله گشتاور-انحنا» (Moment-Curvature Equation) نام دارد. این معادله نشان می دهد که انحنا با گشتاور خمشی M دارای رابطه مستقیم و با کمیت EI رابطه عکس دارد.

EI با عنوان «صلبیت خمشی» (Flexural Rigidity) شناخته می شود. صلبیت خمشی معیاری برای نمایش مقاومت تیر در برابر خمش است.

از این رو، هر چه مقدار این کمیت بیشتر باشد، انحنای تیر برای یک گشتاور خمشی مشخص کمتر خواهد بود. در نهایت توجه داشته باشید که گشتاور خمشی مثبت باعث ایجاد انحنای مثبت و گشتاور خمشی منفی منجر به ایجاد انحنای منفی می شود (شکل زیر).

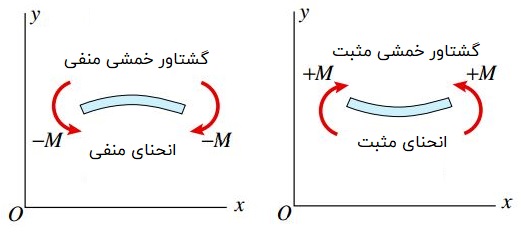
رابطه بین علامت گشتاور خمشی و انحنا