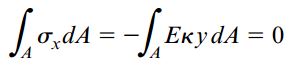تنش های نرمال موجود در تیرها (مختصات محور خنثی)

تنش های نرمال موجود در تیرها (مختصات محور خنثی):
به منظور تعیین اولین معادله استاتیک، المان سطح dA را مطابق شکل زیر در نظر بگیرید. این المان در فاصله y از محور خنثی قرار دارد.

از این رو، تنش اعمال شده بر روی آن (σx) با استفاده از رابطه σx=-Eκy قابل محاسبه خواهد بود. نیروی وارد شده بر المان با σxdA برابر بوده و در هنگام مثبت بودن y به صورت فشاری است.

به دلیل عدم وجود برآیند نیرو بر روی مقطع عرضی، انتگرال σxdA در محدوده A برابر با صفر است:

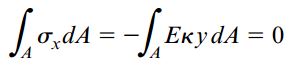
کمیت های انحنا κ و مدول الاستیسیته E، دارای مقادیر ثابت و غیر صفر هستند. به همین دلیل می توان آن ها را از انتگرال بالا حذف کرد. به این ترتیب، خواهیم داشت:

این معادله بیان می کند که گشتاور اول سطح مقطع عرضی حول محور z برابر با صفر است. به عبارت دیگر، محور z از مرکز هندسی مقطع عرضی عبور می کند.

محور z بر روی محور خنثی نیز منطبق است.

بنابراین، اگر ماده از قانون هوک پیروی کند و هیچ نیروی محوری بر روی مقطع عرضی اعمال نشود، محور خنثی از مرکز هندسی سطح مقطع عبور خواهد کرد.

بر اساس این مشاهدات، موقعیت قرارگیری محور خنثی به سادگی تعیین می شود.

توجه داشته باشید که مطالب ارائه شده در این مقاله برای تیرهایی قابل استفاده است که مقاطع عرضی آن ها نسبت به محور y دارای تقارن باشند.

در نتیجه، مرکز مختصات O بر روی مرکز هندسی سطح مقطع قرار خواهد گرفت.

به دلیل تقارن مقاطع عرضی نسبت به محور y، این محور به عنوان یک «محور اصلی» (Principal Axis) محسوب می شود.

محور z نیز به دلیل عمود بودن بر محور y، یکی دیگر از محورهای اصلی خواهد بود.

از این رو، در صورت اعمال خمش خالص بر روی یک تیر از جنس مواد الاستیک خطی، محورهای y و z به عنوان محورهای اصلی مرکزی در نظر گرفته خواهند شد.