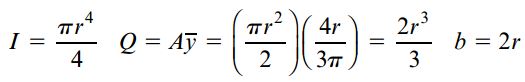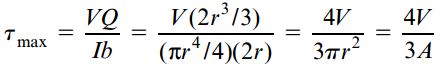تحلیل تنش های برشی در تیرهای دایره ای (سطح مقطع دایره ای)

سطح مقطع دایره ای:
اگر یک تیر مانند شکل زیر دارای سطح مقطع دایره ای باشد، فرض موازی بودن تنش های برشی با محور y صحیح نخواهد بود.

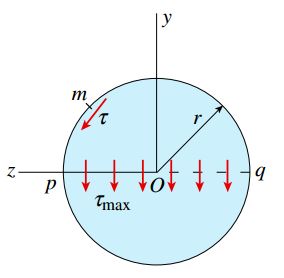
به عنوان مثال، نقطه m بر روی مرز سطح مقطع تیر زیر را در نظر بگیرید. به سادگی می توان اثبات کرد که تنش برشی τ بر روی این نقطه به صورت مماس بر مرز مقطع اعمال می شود.

چراکه در این شرایط مشاهده می شود که سطح خارجی تیر خالی از تنش است و تنش برشی اعمال شده بر روی مقطع عرضی هیچ مؤلفه ای در جهت شعاعی ندارد.

در تحلیل تیرهای دایره ای هیچ راه ساده ای برای تعیین تنش های برشی اعمال شده بر روی کل سطح مقطع وجود ندارد.

اگرچه، با در نظر گرفتن یک سری فرضیات معقول در مورد توزیع تنش می توان مقدار تنش های برشی بر روی محور خنثی را به دست آورد.

به این منظور فرض می کنیم که این تنش ها در راستای موازی با محور y اعمال می شوند و شدت آن ها بر روی عرض تیر (از نقطه p تا نقطه q در شکل بالا) ثابت است.

به دلیل یکسان بودن فرضیات مذکور با فرضیات به کار گرفته شده در رابطه برش (τ=VQ/lb) می توان از این رابطه برای محاسبه تنش های موجود در محور خنثی استفاده کرد.

برای این کار باید کمیت های زیر را به عنوان خصوصیات یک تیر دایره ای با شعاع r به کار برد:

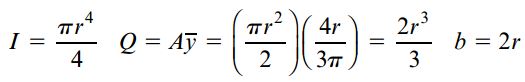
I: ممان اینرسی سطح مقطع دایره ای؛ Q: گشتاور اول؛ b: قطر سطح مقطع

با جایگذاری عبارت های بالا در رابطه برش، تنش برشی ماکسیمم به دست می آید:

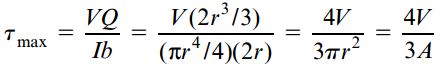
A=πr2: مساحت سطح مقطع

معادله بالا نشان می دهد که تنش برشی ماکسیمم در یک تیر دایره ای، 4/3 برابر میانگین تنش برشی عمودی (V/A) است.