بارهای محوری خارج از مرکز در تیر خمشی

بارهای محوری خارج از مرکز در تیر خمشی:
«بار محوری خارج از مرکز» (Eccentric Axial Load)، باری است که خط اثر آن از روی مرکز هندسی سطح مقطع عبور نمی کند.

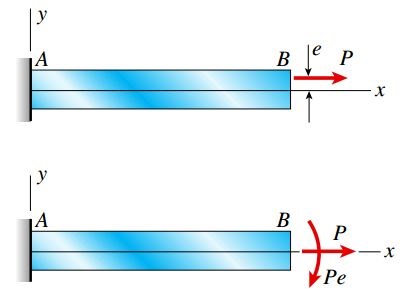
شکل زیر، نمونه ای از اعمال یک بار محوری خارج از مرکز بر یک تیر یکسر گیردار را نمایش می دهد (بار کششی P در فاصله e از محور خنثی x بر روی تیر AB اعمال شده است).

از نظر استاتیکی می توان بار خارج از مرکز P معادلِ یک نیروی محوری اعمال شده در راستای محور x (نیروی P) و یک گشتاور خمشی اعمال شده حول محور z در نظر گرفت (گشتاور Pe). توجه داشته باشید که گشتاور خمشی Pe (در شکل زیر) دارای علامت منفی است.

در شکل زیر، نمای سطح مقطع تیر از رو به رو (عمود بر محور خنثی) نمایش داده شده است. این نما، محورهای y و z گذرنده از مرکز هندسی C را نشان می دهد. بار خارج از مرکز P، با محور y (یکی از محورهای تقارن تیر) تقاطع دارد.

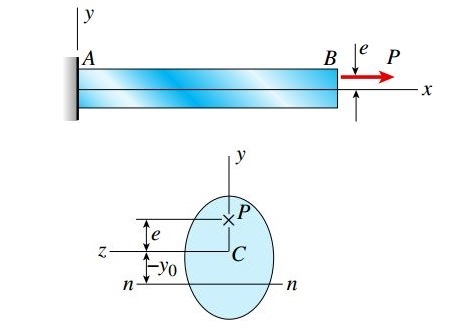
از آنجایی که نیروی محوری N بر روی تمامی مقاطع عرضی با P و گشتاور خمشی با Pe- برابر است، تنش نرمال بر روی هر نقطه دلخواه درون سطح مقطع از رابطه زیر به دست می آید:

A: مساحت سطح مقطع؛ I: ممان اینرسی حول محور z

در شکل زیر، توزیع تنش به دست آمده از رابطه بالا نمایش داده شده است. این شکل، برای شرایطی صدق می کند که P و e دارای علامت مثبت باشند.

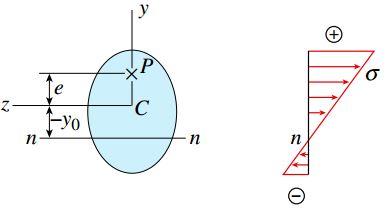
اگر تنش σ در رابطه بالا را برابر با صفر قرار دهیم و معادله به دست آمده را بر حسب مختصات y حل کنیم، محل قرارگیری محور خنثی nn به دست می آید (برای حالتی که P و e مثبت باشند).

به این ترتیب، خواهیم داشت:

برای تعیین مختصات y0، فاصله بین محور z (محور خنثی تحت خمش خالص) تا خط nn با تنش صفر (محور خنثی تحت بارگذاری ترکیبی محوری و خمشی) مورد اندازه گیری قرار می گیرد. به دلیل مثبت بودن y0 در راستای محور y، جهت گیری آن به سمت پایین با y0- نمایش داده می شود.

با توجه به رابطه بالا، به خاطر داشته باشید که برای e مثبت، محور خنثی پایین تر از محور z و برای e منفی، محور خنثی بالاتر از محور z قرار می گیرد.

در صورت کاهش میزان خروج از مرکز، فاصله y0 افزایش می یابد و محور خنثی از مرکز هندسی دور خواهد شد.

با نزدیک تر شدن مقدار e به صفر، محل اعمال بار به سمت مرکز هندسی، محور خنثی به فاصله بی نهایت و توزیع تنش به سمت یکنواخت شدن میل می کند.

در طرف مقابل، افزایش میزان خروج از مرکز باعث کاهش فاصله y0 و نزدیک شدن محور خنثی به مرکز هندسی می شود.

هنگامی که e به یک مقدار بسیار بزرگ می رسد، محل اعمال بار در فاصله بی نهایت قرار گرفته، محور خنثی به مرکز هندسی نزدیک شده و توزیع تنش به شکل توزیع تنش در خمش خالص درمی آید.

نکات تکمیلی:
معرفی تحلیل تیرهای تحت بارهای محوری در این مقاله، با فرض محاسبه گشتاورهای خمشی بدون در نظر گرفتن اعوجاج های تیر صورت گرفت.

به عبارت دیگر، هنگام تعیین گشتاور خمشی M برای به کارگیری در رابطه تنش های ترکیبی باید امکان استفاده از ابعاد اولیه تیر (پیش از رخ دادن هرگونه تغییر شکل یا اعوجاج) فراهم باشد.

این شرایط برای تیرهایی فراهم است که در هنگام اعمال خمش، سختی نسبتاً بالایی از خود نشان می دهند؛ چراکه در این حالت، میزان تغییر شکل و اعوجاج ها بسیار کوچک خواهد بود.

نکته مهم در هنگام تحلیل یک تیر تحت بارهای محوری، ایجاد تمایز بین یک تیر ضخیم (نسبتاً کوتاه و مقاوم در برابر خمش) و یک تیر باریک (طول زیاد و انعطاف پذیری بسیار بالا) است.

برای یک تیر ضخیم و کوتاه، اعوجاج های جانبی به قدری کوچک هستند که هیچ تأثیر قابل توجهی بر روی خط اثر نیروهای محوری ندارند. در این حالت، گشتاورهای خمشی به اعوجاج بستگی نخواهد داشت و تنش های موجود با استفاده از روابط ارائه شده در این مقاله قابل محاسبه خواهد بود.

برای یک تیر باریک و بلند، مقدار اعوجاج های جانبی هر چقدر هم کوچک باشد، برای تغییر قابل توجه خط اثر نیروهای محوری کافی است.

در این حالت، یک گشتاور خمشی اضافی برابر با حاصل ضرب نیروی محوری در اعوجاج جانبی بر روی تمام مقاطع تیر ایجاد می شود. به عبارت دیگر، یک فعل و انفعال یا کوپلینگ بین اثرات محوری و اثرات خمشی به وجود می آید.

وجه تمایز بین یک تیر ضخیم و کوتاه با یک تیر باریک و بلند زیاد واضح و مشخص نیست. به طور کلی، تنها راه تشخیص اهمیت فعل و انفعال اثرات محوری و خمشی، تحلیل تیر با در نظر گرفتن و بدون در نظر گرفتن این مسئله و بررسی میزان اختلاف بین نتایج این دو حالت است.

به عنوان یک راهنمای کاربردی به خاطر داشته باشید که اگر نسبت طول به ارتفاع تیر برابر یا کمتر از 10 بود، می توان آن را به عنوان یک تیر ضخیم در نظر گرفت.

در ادامه به منظور آشنایی بهتر با نحوه تحلیل یک تیر تحت بار محوری، به تشریح کامل یک مثال کاربردی می پردازیم. تیر مورد تحلیل در این مثال به عنوان یک تیر ضخیم در نظر گرفته می شود.