اعمال همزمان بارهای محوری و خمشی

اعمال همزمان بارهای محوری و خمشی:
عضوهای ساختاری اغلب تحت تأثیر همزمان بارهای خمشی و بارهای محوری قرار می گیرند. این شرایط معمولاً در تحلیل قاب های بدنه هواپیما، ستون های ساختمان، ماشین های صنعتی، قطعات کشتی و فضاپیماها قابل مشاهده است.

اگر ضخامت عضوهای تحت بارگذاری خیلی کم نباشد، امکان محاسبه تنش های ترکیبی با استفاده از برهم نهی تنش های خمشی و محوری وجود خواهد داشت.

به منظور آشنایی با نحوه روند تحلیل شرایط مذکور، تیر یکسر گیردار زیر را در نظر بگیرید.

تنها بار موجود بر روی تیر، بار مورب P است که به مرکز هندسی آخرین سطح مقطع اعمال می شود. این بار را می توان به دو مؤلفه (یک بار جانبی Q و یک بار محوری S) تجزیه کرد.

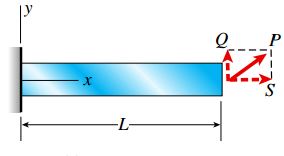
مؤلفه های بار جانبی و محوری، برآیندهای تنش متشکل از گشتاورهای خمشی M، نیروهای برشی V و نیروهای محوری N را همانند شکل زیر درون تیر به وجود می آورند.

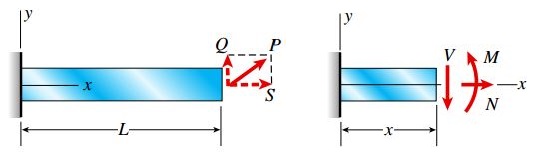
در سطح مقطعی با فاصله x از تکیه گاه، برآیندهای تنش به صورت زیر قابل محاسبه خواهند بود:

L: طول تیر

با به کارگیری رابطه های مناسب نیز می توان تنش های مربوط به هر یک از برآیندهای تنش را تعیین کرد (σ=-My/I، τ=VQ/Ib، σ=N/A). از آنجایی که نیروی محوری N و گشتاور خمشی M باعث ایجاد تنش های نرمال می شوند، با ترکیب این تنش های می توان توزیع تنش نهایی را به دست آورد.

اگر تنها اثر اعمال نیروی محوری N را در نظر بگیریم؛ یک توزیع تنش یکنواخت با میانگین σ=N/A و مشابه شکل زیر بر روی تمام سطح مقطع تیر به وجود می آید. در این مثال به خصوص، تنش σ از نوع کششی بوده و نوع آن با علامت مثبت بر روی شکل نمایش داده شده است.

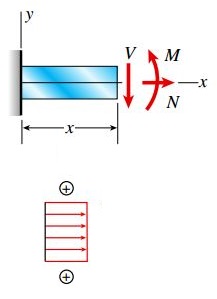
در اثر اعمال گشتاور خمشی نیز یک توزیع تنش خطی با رابطه σ=-My/I و به شکل زیر بر روی سطح مقطع تیر ایجاد می شود. قسمت بالایی تیر تحت فشار و قسمت پایینی آن در معرض کشش قرار می گیرد. فاصله y نسبت به محور z (درون مرکز هندسی سطح مقطع عرضی تیر) اندازه گیری می شود.

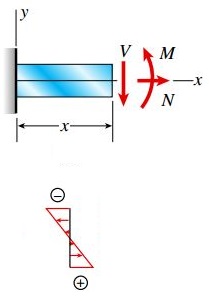
توزیع نهایی تنش های نرمال از برهم نهی تنش های ناشی از نیروی محوری و گشتاور خمشی به دست می آید. بنابراین، معادله تنش های ترکیبی به صورت زیر خواهد بود:

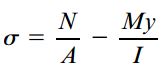
توجه داشته باشید که علامت N به کششی یا فشاری بودن تنش های به وجود آمده بستگی دارد (علامت مثبت برای تنش های کششی و علامت منفی برای تنش های فشاری در نظر گرفته می شود).

علامت M نیز بر اساس قواعد علامت گذاری گشتاور خمشی به دست می آید (گشتاور خمشی مثبت باعث ایجاد فشار در بخش بالایی تیر و کشش در بخش پایینی آن می شود).

علاوه بر این، علامت محور y در جهت رو به بالا مثبت است. اگر از این قواعد علامت گذاری برای رابطه تنش های ترکیبی استفاده کنیم، علامت تنش نرمال σ برای کشش، مثبت و برای فشار، منفی خواهد بود.

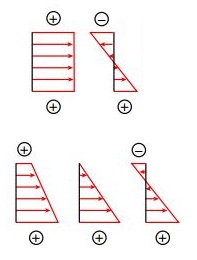
توزیع نهایی تنش به نسبت جبری بین مقادیر هر یک از پارامترهای مرتبط بستگی دارد. برای مثال مورد تحلیل در این مقاله می توان سه احتمال متفاوت را مطابق شکل زیر در نظر گرفت.

اگر تنش خمشی موجود در بالای تیر (شکل بالا چپ) از نظر عددی کمتر از تنش محوری (شکل بالا راست) باشد، نحوه توزیع تنش بر روی مقطع سطح مقطع عرضی مطابق شکل پایین چپ خواهد بود.

در صورت برابر بودن مقدار عددی تنش خمشی موجود در بخش بالایی تیر نسبت به تنش محوری، توزیع نهایی تنش به شکل یک مثلث درمی آید (شکل پایین وسط). حالت سوم زمانی رخ می دهد که مقدار عددی تنش خمشی بیشتر از تنش محوری باشد.

در این حالت همانند شکل پایین راست، بخشی از سطح مقطع در معرض فشار و بخش دیگر در معرض کشش قرار می گیرد. توجه داشته باشید که فشاری بودن نیروی محوری یا معکوس بودن گشتاور خمشی باعث تغییر نسبی توزیع تنش می شود.

هرگاه بارهای خمشی و محوری به صورت همزمان بر روی یک سازه اعمال شوند، محور خنثی (خطی بر روی مقطع عرضی با تنش نرمال صفر) از مرکز هندسی سطح مقطع عبور نخواهد کرد. در شکل بالا نیز می توان مشاهده کرد که محور خنثی در هر یک از مثال ها با یکدیگر تفاوت دارد.

این محور برای حالت اول خارج از مقطع عرضی، برای حالت دوم در گوشه مقطع و برای حالت سوم درون مقطع قرار گرفته است. در مثال انتهای این مقاله، نحوه به کارگیری این نکات را به منظور تعیین تنش های موجود در یک تیر تحت بارهای محوری را به طور کامل تشریح خواهیم کرد.